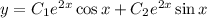Знайти загальний розв’язок лінійних однорідних ДР 2-го порядку зі сталими коефіцієнтами(Завдання на фото)
Другие вопросы по теме Математика
Популярные вопросы
- 30 алина, мария и елена посетили канцелярский магазин. алина решила...
2 - рома разделил мандарин на несколько разных долек. сначала он съел...
1 - Какое частное бльше? [tex]558 \div 9[/tex] ...
2 - Любовь думал я сильнее смерти и страха. только ей только любовью...
1 - П.15 развернутый план,окончание смуты,новая династия...
3 - Перпендикуляры к сторонам, равным 30 и 40, равны соответственно...
2 - Какие реки, озёра, горы, города есть в вашей местности? сравните...
3 - Какие целые числа заключены между числами -3.1 и 0.86; -10.9 и...
3 - какая из точек зрения на происхождение названия россия кажется...
1 - Найти i для данной ( только формулы )...
3
Рівняння вигляду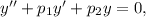 де
де 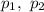 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді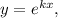 де
де 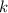 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 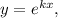 то
то 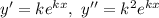
Можливі три випадки:
➀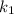 і
і 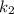 — дійсні,
— дійсні, 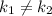
Фундаментальна система розв'язків: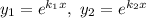 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 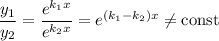
Загальний розв'язок: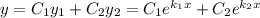
Приклад: а)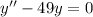
Метод Ейлера: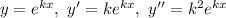
Характеристичне рівняння: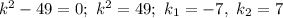
Загальний розв'язок: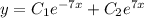
Відповідь: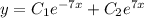
Приклад: в)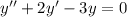
Метод Ейлера: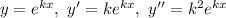
Характеристичне рівняння: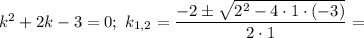
Загальний розв'язок: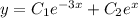
Відповідь: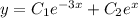
➁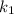 і
і 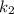 — дійсні,
— дійсні, 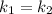
Якщо покласти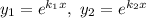 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 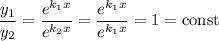
Фундаментальна система розв'язків: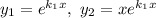 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 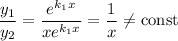
Загальний розв'язок: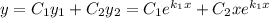
➂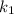 і
і 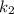 — комплексно спряжені,
— комплексно спряжені, 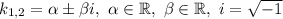
Фундаментальна система розв'язків: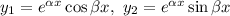 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 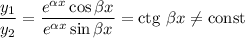
Загальний розв'язок: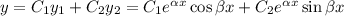
Приклад: б)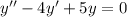
Метод Ейлера: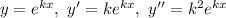
Характеристичне рівняння: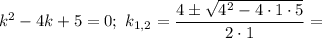
Отже,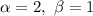
Загальний розв'язок: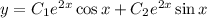
Відповідь: