1. Математика
  2. Знайти загальний розв язок

Знайти загальний розв'язок диференціального рівняння x^2*y''+6y'+6y=0 якщо відомий його частинний розв язок y=x^-2

sergsjvashhuk sergsjvashhuk    1   14.06.2019 14:57    0

Ответы
Наталья0201 Наталья0201  02.10.2020 01:50

Застосуємо формулу Ліувілля-Остроградського.

\displaystyle \int^x_{x_0}\dfrac{6}{t^2}dt=-\dfrac{6}{t}\bigg|^x_{x_0}=-\frac{6}{x}+\frac{6}{x_0}

\left|\begin{array}{ccc}y_1& y_2\\ y_1'& y_2'\end{array}\right|=W_0(x)e^\big{-\frac{6}{x}+\frac{6}{x_0}}=\dfrac{W_0(x)}{e^\big{-\frac{6}{x_0}}}\cdot e^\big{-\frac{6}{x}}=C_1e^\big{-\frac{6}{x}}

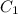де C_1 — постійна константа.

За означення визначника, отримаємо

y'_2y_1-y_2y_1'=C_1e^\big{-\frac{6}{x}}~~~~\Rightarrow~~~~\dfrac{y_2'y_1-y_2y_1'}{y_1^2}=\dfrac{C_1e^\big{-\frac{6}{x}}}{y_1^2}\\ \\ \bigg(\dfrac{y_2}{y_1}\bigg)'=\dfrac{C_1e^\big{-\frac{6}{x}}}{y_1^2}=\dfrac{C_1e^\big{-\frac{6}{x}}}{(x^{-2})^2}=C_1x^4e^\big{-\frac{6}{x}}\\ \\ \displaystyle \frac{y_2}{y_1}=\int C_1x^4e^\big{-\frac{6}{x}}dx~~~~\Rightarrow~~~\boxed{y_2=x^{-2}C_1\int x^4e^\big{-\frac{6}{x}}dx}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Kirich0ult Kirich0ult  21.10.2020 19:35
А) А(-7);В(2) Ә) С(-5);D(1) Б)Е(-6);F(-2)В)K(-4);L(0) дам 10 бИ решать 1 и 2​...
VictorBo VictorBo  21.10.2020 19:35
узнаи обьем коропки если ее длина 15 см ширина 10 см высота 10см?наидй сумму площадей боковых граней коробкой?​...
Николо223 Николо223  21.10.2020 19:35
Из четырёх одинаковых треугольников можно составить три фигуры, изображённые на рисунке. Периметр одной из фигур равен 50 см. Найдите периметры двух других фигур, если известно,...
ruslan5632 ruslan5632  21.10.2020 19:36
Длина прямоугольника равна 90мм,а ширина на 11 см больше. Найдите периметр и площадь прямоугольника решить задачу...
Оленька090 Оленька090  21.10.2020 19:36
Довести, що пряма AB проходить через початок координат, якщо A(-3;2) B(9;-6)...
vasilevamarin vasilevamarin  21.10.2020 19:47
Мына есепті түсінбедім айтып жіберіңдерш​...
anton1oleynik anton1oleynik  21.10.2020 19:47
355.1)-5/6жəне-8/3помагите домашку...
LIZA31012006 LIZA31012006  21.10.2020 19:47
1). 10 3/23 - 7 19/46 = ? 2). 16 2/5 - 4 3/7 = ? 3). 19 5/12 - 8 17/18 = ?...
calusiker calusiker  21.10.2020 19:47
Ядро казахской интеллигенции​...
xelasaa48 xelasaa48  21.10.2020 19:47
решить Хотя бы одно из заданий...

Популярные вопросы