Знайти похідну функції Найти производную функции
y=\frac{1}{2} (arcsin\frac{x-1}{\sqrt{2} }+x) 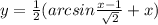
Другие вопросы по теме Математика
Популярные вопросы
- Bob and anna are talking about something....
1 - Две одинаковые сферы имеют заряды: q1=+3.2×10 в 10 степени е; q2=-3.8×10 в...
2 - Напишите краткое сочинение о рассказе любовь чехова на оценку 3-4...
3 - На ремонт школы купили 20банок 60литров белой краски . что бы.120кг.красной...
3 - Нужна горизонтальная схема предложения как ни был он подготовлен, сердце ёкнуло:...
1 - Велосипедист проехал 60 км за 5 часов за какое время он проедет этот путь если...
3 - Выражение -3 * корень из (0,25 * y^2) если y либо = 0...
1 - Шпапнлраашещро пшнсеоанило ншмлднпдгпо гдпгдпг...
1 - Підскажіть будьласка якесь речення до слова п*ятисотий зарано дякую!...
2 - ответьте на вопросы по , заранее буду . ( 20 ! ) 1.в какой части греции находится...
2
Пошаговое объяснение: