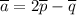Знайти подання вектора a=5i+4j у базисі p; q, де p=2i+3j; q=-i+2j
Другие вопросы по теме Математика
Популярные вопросы
- 17. В июле 2025 года планируется взять кредит 600тыс. на 6 лет....
2 - Напишите сходство и различия Абхазия , Аджария и Гурия....
2 - Решите уравнение 19x^4-10x^3+1x^2-10x+19=0...
1 - ів! До іть будь ласка Семінар/презентація на тему «Енегрія біомаси»...
2 - 863. Сколько сантиметров: а) в четвярти метра;б) в десятой доле...
3 - В двовимірному масиві замінити всі елементи що макють парні...
2 - выбрать правильный вариант. Robert didn’t answer the phone when...
1 - Упростить выражение cos(п+a)+sin(п/2+a) а) 0 б) -cosa+sina в)...
1 - Чему равно значение выражения (2^-0,7)^-0,7*(0,5)^3,49...
2 - Sin2x-cosx+2=0 и указать корни, принадлежащие промежутку [0;π]...
1
Для начала проверим образуют ли вектора базис.
Поскольку определитель матрицы не равен нулю, то наша система векторов является базисом.
ответ: