Знайти частинний розв’язок диференціального рівняння.
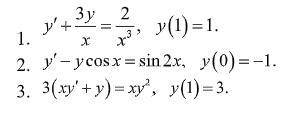
Другие вопросы по теме Математика
Популярные вопросы
- Какие сказания о богах и о героях греции вы знаете?...
2 - Художественного произведения с вводными словами и предложение...
1 - Вообщем,случилась на днях такая отличница,6 класс)по обществознанию всегда...
1 - Два пешехода одновременно вышли навстречу друг другу из двух пунктов. первый...
1 - Укажіть кількість речовини оксигену у 0,5 моль сульфатної кислоти: а)1,5;...
1 - Діти катаються на санчатах. діти катаються на лижах. веселиться дітвора!...
2 - Смесь гидроксидов натрия и калия массой 2,72 г. обработали серной кислотой,...
3 - Вкаком имени содержится кознание на меру веса...
2 - Сколько литров молока было в банке,если после того,как из банки вылили...
1 - Напишіть формули оксидів , які відпові а)сульфатній , б)сульфітній і в)силікатній...
2
1
общее решение
частное решение
2.
общее решение
частное решение
3.
общее решение
частное решение