Знайдить уси пары такых натуральных чысел х та у що ( нсд(х,у))2=ху

Для всех равных пар натуральных чисел

Пошаговое объяснение:

Пусть канонические виды чисел x и y таковы:

где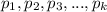  - простые числа, а

- целые неотрицательные степени простых чисел (некоторые могут равняться нулю).

Тогда по свойству НОД(x; y)=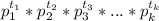

где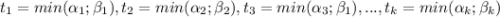

По условию НОД(x; y)²=x · y и отсюда следует, что

Очевидно, что значение min(m; n) или m или n. Поэтому, если

, то из равенства следует, что и . Точно такое равенство можно установить если .

И такие равенства получаются для других степеней простых чисел.

Отсюда заключаем, что НОД(x; y)²=x · y, тогда и только тогда, когда x=y.

Отсюда следует ответ к задаче: для всех равных пар натуральных чисел.