1. Математика
  2. Знайдіть суму нескінченної

Знайдіть суму нескінченної ї прогресії 125; -25; 5; …

769429 769429    3   27.09.2019 01:20    0

Ответы
Роорш Роорш  08.10.2020 21:34

Знаменатель прогрессии: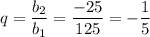 q=\dfrac{b_2}{b_1}=\dfrac{-25}{125}=-\dfrac{1}{5}


Сумма бесконечно убывающей геометрической прогрессии:


S=\dfrac{b_1}{1-q}=\dfrac{125}{1+\dfrac{1}{5} }= \dfrac{625}{6}

ПОКАЗАТЬ ОТВЕТЫ
Timofry Timofry  08.10.2020 21:34

q = b2/b1 = -25/125 = -1/5

S = b1/(1 - q) = 125 : (1 - (-1/5)) = 125: (1 + 1/5) = 125 : 6/5 = 125 * 5/6 = 625/6

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
gribvlad123 gribvlad123  29.08.2019 08:40
Укакого числа делится на 3 с остатком? а)245 б)348 с)12342...
лошадь20 лошадь20  29.08.2019 08:40
Решите уравнения 4у-5,8=18,4 32+(z-5,38)=26,62...
миша1089 миша1089  29.08.2019 08:40
2. найдите значение выражения. 180848 : 356 + 763 х 134 – 33078...
2017minikot 2017minikot  29.08.2019 08:40
Вмагазин 15 коробок конфет и печенья 8 ящиков чего больше и на сколько...
Элиана01 Элиана01  29.08.2019 08:40
Было 7 листов бумаги.некоторые из них разрезали на 7 частей,потом некоторые ещё разрезали на 7 частей, и такие действия повторили несколько раз. могло ли в результате получиться...
Bened Bened  29.08.2019 08:40
Вычислите объем куба с ребром 1/4 м (дробь)...
Shepinvan912 Shepinvan912  29.08.2019 08:40
3+5= (5²+5²): 5)²= (4²+4)*5-10²+1= -100+101+4²+21: 7= (-1+2-3+4-5+6-7+8-9+10)²= решите!...
хеллокиттичка хеллокиттичка  29.08.2019 08:40
Площадь поля 8 ар 250кв метров засеяли соей а остальное поле заняли под проссо какую площадь засеяли проссом...
ROLBER ROLBER  29.08.2019 08:40
Одновременно с 2 сел расстояние между которыми 24 км, отправились на встречу друг другу велосепедист и пешеход через 1.5 часа они встрелитились определите скорость пешехода...
denisfilin2 denisfilin2  29.08.2019 08:40
Упродавца есть шестиметровый кусок ткани. первая покупательница попросила отрезать ей кусок ткани длиной 3 м 55 см, а вторая - длиной 150 см. кусок ткани какой длины останется...

Популярные вопросы