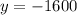Знайдіть рівняння горизонтальної дотичної до графіка функції f(x) = (5^x - 65)(5^x + 15)
Другие вопросы по теме Математика
Популярные вопросы
- Как движется спутник, первой космической скоростью? второй космической...
2 - Ккакому семейству относятся семейства розоцветных...
2 - Боковые рёбра треугольной пирамиды взаимно перпендикулярны и соответственно...
1 - Папа купил телевизор на распродаже за 24330 рублей. сколько стоил телевизор...
1 - Втреугольнике авс угол с равен 90 косинус в равен 2/5 ав=10 найдите вс...
3 - Указать часть речи каждого слова в тексте. маленький (прилаг.) ёжик (сущ.)...
2 - Вдвух отрезах 64 м ткани, причём во втором отрезе на 16 м меньше, чем...
3 - С# в трехзначном числе x зачеркнули первую цифру. когда оставшееся число...
3 - Брошены 2 игральные кости. найдите вероятность того, что произведение...
2 - 7/12×18/14 и дайте не просто ответ,но и решение...
3
Уравнение касательной имеет вид:
где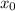 — абсцисса точки графика функции
— абсцисса точки графика функции 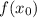 , к которому проведена касательная
, к которому проведена касательная 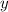 .
.
Так как график касательной имеет вид график прямой линейной функции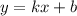 , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции — 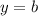
Таким образом, касательная будет горизонтальной, если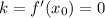
Найдем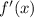 :
:
Найдем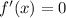 :
:
Следовательно,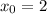 — абсцисса точки графика функции
— абсцисса точки графика функции 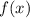 , к которому проведена касательная
, к которому проведена касательная 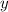 .
.
Найдем значение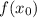 :
:
Таким образом,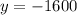 — уравнение горизонтальной касательной к графику функции
— уравнение горизонтальной касательной к графику функции 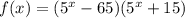
ответ: