Знайдіть проміжки зростання, спадання та точки екстремуму функції у=3х-х³
Другие вопросы по теме Математика
Популярные вопросы
- Сколько лет не виделись Деев и Лёнька? Симонов «Сын артиллериста»...
1 - Народные движения и восстания XVII века, указать причины, основные итоги и значение...
1 - Шар массой 4 кг на высоте 3 м обладает полной механической энергии 150 Дж. Чему...
2 - РЕБЯТА АНГЛИЙСКИЙ ЯЗЫК БЫЛЫ ...
2 - Вставьте пропущенные слова в текст предложения. Главные принципы, гарантирующие...
2 - На какие фазы можно разделить баскетбольный бросок? А) решающая, заключительная...
3 - Определите, сколько букв Н пишется в следующих словах. клеё..ый брус сыровяле..ая...
3 - Найдите значение выражения (x -^3)^4 · 4x^13, если x = 4...
3 - Визначте похідні слова сніговик; сніг; сніжна....
2 - ОБЖ кр, как можно скорее!! Много Как правильно отпугивать коронувирас (септиантики,...
1
Найдём производную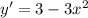
В нулях производной будут экстремумы
x = 1, x = -1 - точки экстремума, при x > 1 - производная отрицательна, поэтому функция убывает, при -1 < x < 1 - производная положительна, поэтому функция возрастает, ну x < -1 - производная отрицательна, функция убывает.
ответ: [1;+∞) - функция убывает, [-1;1] - возрастает, (-∞;-1] - убывает, x=-1 - точка минимума, x=1 - точка максимума