Знайдіть область визначення функції
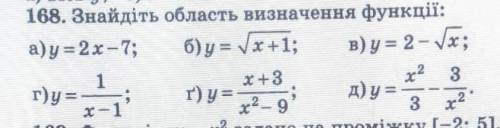
Другие вопросы по теме Математика
Популярные вопросы
- В. д. герасимов тест для самопроверки номер 10 если 64 метра ситца стоят столько...
1 - На доске написаны числа от одного до 299 раз в минуту какие-то два часа стираются...
2 - Вданном ниже ряду слов найди слово в котором все согласные звуки звонкие выпиши...
3 - Какое вещество в данном состоянии не имеет собственной формы и занимает определённый...
2 - Как будет по , ученица которая учится на тройки (троечница)? ответте ! )...
3 - Для приготовления клубничного варенья требуется 5 частей ягод, 6 частей сахара...
1 - 9прочитай и отметь (м) правильный вариант.1 did susie play football last saturday?...
3 - Втзначте індуктивність котушки, в якій під час зміни сили струму від 10 до...
1 - 2000 дм3 =8 000 дм3 =3 000 см3 =90 000 дм3 =7 000 дм3 =...
3 - Алишер со скоростью 10 км/ч шёл 6 ч. скорость шерали на 50 км/ч больше, чем...
1
Пошаговое объяснение:
Область определения любой функции не должна включать такие значения переменной, при который выражение не будет иметь смыста - перечислю основные
1) деление на 0
2) вычисления корня из отрицательного числа
3) логарифмирование отрицательного числа
Область значения - все значения, которые может принимать функция
Итак, приступим к выполнению задания
1) Посмотрим на функцию: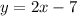
Никаких запрещённых операций нет. Так что
2) Посмотрим на функцию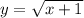
Есть корень, значит подкоренное выражение (х + 1) должно быть больше или равно 0. Запишем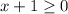 или
или 
Так как корень всегда положителен, то его значение всегда больше или равно 0.
3) Посмотрим на функцию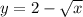
Видим корень, значит подкоренное выражение всегда больше или равно 0. Запишем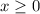
Так как корень всегда положителен, тогда
Тогда значения функции меньше или равны 2
4) Посмотрим на функцию: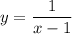
Тут есть деление, значит мы не делим на 0, т.е.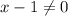 или
или 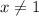
Тогда значения в точке 0 у функции не будет (числитель дроби 1)
5) Посмотрим на функцию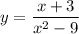
Здесь дробь. Тогда знаменатель не 0. То есть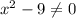 . Запишем
. Запишем
Дробь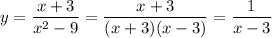 не может быть равна 0 так как числитель не 0.
не может быть равна 0 так как числитель не 0.
Тогда
6) Посмотрим на функцию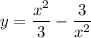
Здесь есть дробь, значит сразу знаменатель не равен 0.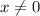
Преобразуем дробь.
Дробь определена при любых х, тогда