Знайдіть найбільше і найменше значення функції на відрізку [а, б]
Популярные вопросы
- Что такое природное сообщество для 3 класса...
3 - Внешняя политика екатерины ii подробный план )...
3 - Вкоробке были карандаши. сначала из коробки взяли 50% карандашей, а...
3 - Выписать из учебника по 2предложения сложно подченёное...
2 - Какие художественные детали дает чехов в описание семьи туркиных...
1 - Предложите несколько классификаций перечисленных организмов. назовите...
1 - What important things do you think i should take? в поход ответ двумя...
2 - Какие типы клеток выделяют у сфагнума? какие функции выполняют эти клетки?...
3 - В) 12x+x-14x= г) a-4a+9a= д) -6a+6a+4a= е) -4x+8x-x=...
3 - Вчетырёх больших пакетах лежат груши, по 20 в каждом, а в трёх маленьких...
2
Найти наибольшее и наименьшее значение функции y=x^3-3x^2-9x+35 на промежутке [-4;4].
ответ:Наибольшее значение функции на промежутке [-4;4] - y(-1)=40; наименьшее - у=(-4)=(-41).
Пошаговое объяснение:Для начала вспомним теорию. Алгоритм нахождения наибольшего и наименьшего значений функции на заданном промежутке:
Найти производную ф-ции. Находим критические точки, которые принадлежат заданному промежутку.Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.Выбираем наибольшее и наименьшее из них.1. Найдём производную функции.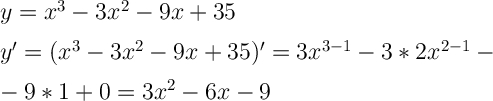
2. Находим критические точки, которые принадлежат заданному промежутку.![\Large \boldsymbol {} x\inx\in(-\infty;+\infty)3x^2-6x-9=0D=b^2-4ac=(-6)^2-4*3*(-9)=36+108=144x_{1,2}=\frac{-b\pm\sqrt{D} }{2a} x_1=\frac{-(-6)+\sqrt{144} }{2*3} =\frac{6+12}{6} =\frac{18}{6} =3\in[4;4]x_2=\frac{-(-6)-\sqrt{144} }{2*3} =\frac{6-12}{6} =\frac{-6}{6} =-1\in[4;4]](/tpl/images/4977/5099/33aef.png)
3. Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.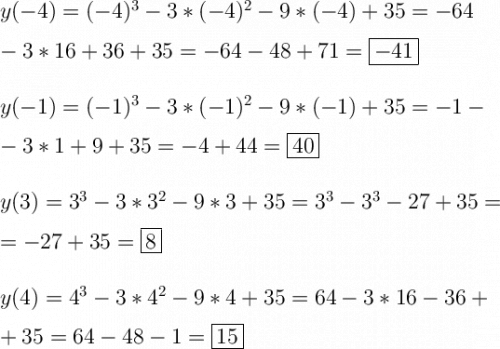
4. Выбираем наибольшее и наименьшее из получившихся значений: