Знайдіть кут між стороною AC і медіаною BB1 трикутника ABC, якщо A(3;5;0) B(0;-6;0) C(3;1;0)

Ответы

artemka222288 17.07.2021 13:23

arccos(0,9)≈26°

Пошаговое объяснение:

Заданий кут буде дорівнювати куту між векторами В1B і АС.

Вектор АС=(3-3; 1-5; 0-0)=(0; -4; 0).

В1=(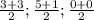 $\frac{3+3}{2};\frac{5+1}{2} ;\frac{0+0}{2}$ )=(3; 3; 0).

Вектор В1В=(0-3; -6-3; 0-0)=(-3; -9; 0).

$cos(AC, B_{1}B)=\frac{AC*B_{1}B}{|AC|*|B_{1}B|} =\frac{0*(-3)+(-4)*(-9)+0*0}{\sqrt{0^{2}+(-4)^{2}+0^{2}} *\sqrt{(-3)^{2}+(-9)^{2}+0^{2}} } =\frac{36}{4*10} =0,9$

∠(AC, B1B)=arccos(0,9)≈26°

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Клямпер 08.05.2021 23:19

Микола й петро купили декілька однакових конструкторів.Микола заплатив 85 грн,а Петро на 34 грн більше.Скільки коштує один конструктор?...

evgenijstepano 08.05.2021 23:21

. установити відповідність1) 1 4^х 642) 0,5^х 0,1253) 3 3^х 274) 0,1^х 0.001А) (-3; +&)Б) (0;3)В) (1;3)Г) (-&;3)Д) (3;+&)(& - це безконєчность)...

ilyapleshakov29 08.05.2021 23:23

. Укажіть найбільший цілий розв язок нерівності log0.2(3-2x)= 1Варіанти відповіді:A) -2Б) -1В) 1Г) такого розв язку не існує ...

mansurevk2005 08.05.2021 23:32

Задание 2. Запиши двойные неравенства и рядом в квадратныхСкобках их решенияt больше 15 и меньше 22а больше 73 и меньше 85у больше 5 и меньше 14...

Silwashka99 08.05.2021 23:33

Область визначення функціїy=7/7^x-1...

AnastasyaOrlyanskaya 08.05.2021 23:33

Знайти множину розв язків нерівностей0.6^x2 0.6...

кирилл5775065421423 08.05.2021 23:34

Робітник обслуговує три верстати. Ймовірність того, що протягом години його уваги буде потребувати перший верстат, дорівнює 0,7, другий- 0,5, третій- 0,75. Визначити ймовірність...

Irishagogo 08.05.2021 23:37

НАЙТИ СУММУ ДАННЫХ МНОГОЧЛЕНОВ. ПУНКТ А)...

AlinaRaytman 09.05.2021 00:04

Задание 3. Реши геометрическую задачу. (краткая запись, решение,ответ)Высота прямоугольногопараллелепипеда 52 см, длина в 3раза больше, а ширина на 56 смменьше длины. Найди объём...

DestroyMe 09.05.2021 00:04

Тема : визначення інтегралів Знайти площу фігури обмеженої лініями...

Знайдіть кут між стороною AC і медіаною BB1 трикутника ABC, якщо A(3;5;0) B(0;-6;0) C(3;1;0)

Популярные вопросы