1. Математика
  2. Здравствуйте с решением

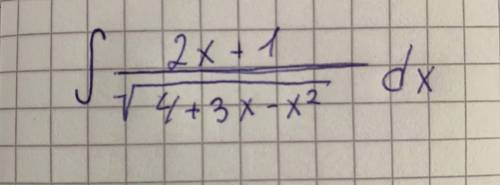
Здравствуйте с решением примера. Самому никак не получается решить. Заранее за


Здравствуйте с решением примера. Самому никак не получается решить. Заранее за

gordeevlogain2 gordeevlogain2    2   24.01.2021 16:41    0

Ответы
лехакек лехакек  23.02.2021 16:42

Пошаговое объяснение:

перепишем 2х+1 как 2х-3+4, тогда получим два интеграла

\displaystyle \int {\frac{2x-3}{\sqrt{-x^+3x+4} } } \, dx +\int {\frac{4}{\sqrt{-x^+3x+4}} } \, dx

теперь в первом интеграле можем заметить, что числитель есть производная от знаменателя только со знаком минус. заменим (-х² +3х+4) = u, тогда du=-(2x-3)dx

и вот первый интеграл превратится в табличный

\displaystyle \int {\frac{2x-3}{\sqrt{-x^+3x+4} } } \, dx=-\int {\frac{1}{\sqrt{u} } } \, du =-2u+C = -2\sqrt{-x^2+3x+4} +C

теперь разберемся со вторым интегралом. у него выделим в знаменателе полные квдраты и получим тоже табличный интеграл

\displaystyle 4\int {\frac{1}{\sqrt{-x^+3x+4}} } \, dx= 4\int {\frac{1}{\sqrt{(\frac{5}{2} )^2-(3-\frac{3}{2})^2 } } } \, dx

это интеграл вида

\int {\frac{1}{\sqrt{a^2-x^2} } } \, dx = arcsin(\frac{x}{a}) +C

и тогда наш второй интеграл

\displaystyle 4\int {\frac{1}{\sqrt{(\frac{5}{2} )^2-(3-\frac{3}{2})^2 } } } \, dx = 4arcsin(\frac{2x}{5} -\frac{3}{5} )+C

теперь получим результат

\displaystyle \int {\frac{2x+1}{\sqrt{4+3x-x^2} } } \, dx = -2\sqrt{4+3x-x^2} + \displaystyle 4arcsin(\frac{2x}{5} -\frac{3}{5} )+C_1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Умару11 Умару11  13.05.2020 17:24
X-2/x-7=5/8 найдете корень​...
Влад32321 Влад32321  13.05.2020 17:24
В параллели четвёртых классов 150 человек. Пятая часть всех четвероклассников не посещают школьную библиотеку. Сколько учеников четвёртых классов не посещают библиотеку...
TheFelixShow TheFelixShow  13.05.2020 17:24
Уменши 1 дм² на 3 см².какая величина получится?...
янивановсергеевич янивановсергеевич  13.05.2020 17:24
решите хоть что-то я плачу 3 часа я за вас свечку в церкви поставлю80 куб.м 50 куб.дм=... куб.дм18 куб.дм=...л7000 куб.мм=куб.см8л=... куб.см14000 куб.мм=... куб.см2...
NiKoOl18 NiKoOl18  13.05.2020 17:24
Докажите, что функция F есть первообразная для функции f на заданном промежутке: F(x) = x5, f(x) = 5x4, xϵ(-∞;+∞). 2. Является ли функция F первообразной для функции...
Gkdm Gkdm  13.05.2020 17:24
На координатной плоскости дана точка с координатами (6;8).Которые из данных координат являются координатами точки, симметричной данной точке относительно оси ординат...
dpa2807 dpa2807  13.05.2020 17:24
5. Выберите верные утверждения: 1) У пирамиды два основания. 2) Высота прямой призмы равна боковому ребру. 3) У правильной пирамиды основание правильный многоугольник....
Vikamurzikk Vikamurzikk  13.05.2020 17:24
ш Напишите уравнение касательной к графику функции у = х^2 - 2х + 5 в точке х0 = -1...
Mv0856 Mv0856  13.05.2020 17:24
Только нормальные ответы ​...
alexalu0402 alexalu0402  13.05.2020 17:24
1.В книге напечатаны рассказ и повесть, которые вместе занимают 75 стр.Повесть занимает в 2 раза больше страниц, чем рассказ.Сколько страниц занимает рассказ и сколько...

Популярные вопросы