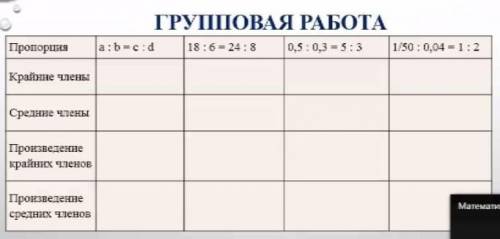
Заполните таблицу: пропорция, крайние члены , средние члены, произведения крайних членов, произведения средних членов

Добрый день! Рад помочь вам с решением математической задачи.

Дана таблица с пропорцией, крайними и средними членами, произведениями крайних и средних членов. Наша задача - заполнить ее.

Давайте разберемся, что такое пропорция. Пропорция - это соотношение двух отношений или двух дробей, которые равны между собой. В нашем случае, пропорция содержит две пары отношений: 4:5 и 8:10. Оба этих отношения равны, поэтому можно составить пропорцию:

4:5 = 8:10

Теперь найдем крайние и средние члены в каждом отношении. В каждом отношении, крайние члены - это числа, стоящие в начале и в конце отношения. В нашем случае, крайние члены в первом отношении 4:5 - это 4 и 5, а во втором отношении 8:10 - это 8 и 10.

Средние члены - это числа, стоящие между крайними членами в отношении. В нашем случае, средние члены в первом отношении - это "?", а во втором отношении - это "?".

Теперь рассмотрим произведение крайних и средних членов. Произведение крайних членов в пропорции равно произведению первого крайнего члена с вторым крайним членом в пропорции. В нашем случае, произведение крайних членов в первом отношении 4:5 - это 4 * 5 = 20, а во втором отношении 8:10 - это 8 * 10 = 80.

Произведение средних членов в пропорции равно произведению первого среднего члена с вторым средним членом в пропорции. В нашем случае, произведение средних членов в первом отношении - это "?" , а во втором отношении - это "?".

Имея все это в виду, заполним таблицу:

| Пропорция | Крайние члены | Средние члены | Произведение крайних членов | Произведение средних членов |
|-----------|---------------|---------------|----------------------------|---------------------------|
| 4:5 | 4, 5 | ?, ? | 4 * 5 = 20 | ?, ? |
| 8:10 | 8, 10 | ?, ? | 8 * 10 = 80 | ?, ? |

Как видите, нам необходимо найти значения средних членов в каждом отношении. Для этого мы можем использовать правило: средний член равен произведению крайних членов, деленному на другой крайний член. То есть:

Средний член = Произведение крайних членов / Другой крайний член

Применяя это правило, заполним оставшиеся значения в таблице:

| Пропорция | Крайние члены | Средние члены | Произведение крайних членов | Произведение средних членов |
|-----------|---------------|---------------|----------------------------|---------------------------|
| 4:5 | 4, 5 | 4/5, ? | 4 * 5 = 20 | (4/5)*? |
| 8:10 | 8, 10 | 8/?, ? | 8 * 10 = 80 | (8/10)*? |

Осталось только решить два уравнения и найти "?" в каждом случае.

В первой строке у нас есть уравнение:

4/5 = 8/?

Чтобы найти значение "?", мы можем использовать кросс-мультипликацию. Возьмем попарные произведения крайних членов и приравняем их:

4 * ? = 5 * 8

Решим это уравнение:

4 * ? = 5 * 8

? = (5 * 8) / 4

? = 40 / 4

? = 10

Таким образом, мы нашли значение среднего члена в первом отношении - это 10.

Аналогичным образом, решим второе уравнение:

8/? = 80/?

?(8) = ?(80)

? = (80 * 8) / 10

? = 640 / 10

? = 64

Таким образом, мы нашли значение среднего члена во втором отношении - это 64.

Окончательно заполнив таблицу, получим:

| Пропорция | Крайние члены | Средние члены | Произведение крайних членов | Произведение средних членов |
|-----------|---------------|---------------|----------------------------|---------------------------|
| 4:5 | 4, 5 | 4/5, 10 | 4 * 5 = 20 | (4/5)*10 |
| 8:10 | 8, 10 | 8/64, 64 | 8 * 10 = 80 | (8/10)*64 |

Надеюсь, что получившийся ответ понятен и помог вам в решении задачи. Если у вас остались вопросы, пожалуйста, не стесняйтесь задавать их.