1. Математика
  2. Запишите упование окружности

Запишите упование окружности радиусом 2√2, которая проходит через точки c(-3; -1) и d(1; -1)
(только а)

daulrtutegenov1 daulrtutegenov1    2   19.11.2019 11:25    2

Ответы
artyom2980 artyom2980  10.10.2020 14:14

(x+1)^2+(y-1)^2=8

или

(x+1)^2+(y+3)^2=8

Пошаговое объяснение:

Пусть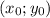 (x_0;y_0) - центр окружности, r - радиус окружности.

Уравнение окружности: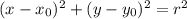 (x-x_0)^2+(y-y_0)^2=r^2

Так как точки C и D лежат на окружности, а радиус равен 2√2, то:

\left \{ {{(-3-x_0})^2+(-1-y_0)^2=(2\sqrt{2})^2 \atop {(1-x_0})^2+(-1-y_0)^2=(2\sqrt{2})^2}} \right.

\left \{ {{(x_0+3})^2+(y_0+1)^2=8 \atop {(x_0-1})^2+(y_0+1)^2=8}} \right.

Вычтем из первого уравнения второе, получим:

(x_0+3)^2-(x_0-1)^2=0,\\(x_0+3-x_0+1)(x_0+3+x_0-1)=0,\\2x_0+2=0,\\x_0=-1

Далее найдем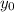 y_0:

(-1+3)^2+(y_0+1)^2=8,\\(y_0+1)^2=4\\y_0+1=\pm 2,\\(y_0)_1=-3\\(y_0)_2=1

Тогда возможно два уравнения окружности:

(x+1)^2+(y-1)^2=8

или

(x+1)^2+(y+3)^2=8

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
LIZA555666777 LIZA555666777  08.06.2020 02:28
В тигриной семье трое тигрят. Они родились в один день, но, возможно, в разные годы. В день их рождения папа-тигр обнаружил, что их суммарный возраст в 5 раз больше, чем был суммарный...
YerasylAmangeldi YerasylAmangeldi  08.06.2020 02:27
Найти экстремум функции f(x,y) X^6+x^4y-2x^4-x^2y-y^2+2y...
kozlovvlad21 kozlovvlad21  08.06.2020 02:27
ВПМ, студенты решить практические, до вечера (сегодня) нужно сдать. Безумно буду благодарен!...
Lizalalaz305 Lizalalaz305  08.06.2020 02:27
В компании 6 человек. Может ли быть так, что у всех разное число знакомых в этой компании? б) А если в компании 7 человек...
Larisa150301 Larisa150301  08.06.2020 02:27
решить данные задания,желательно с фото решения,если можно)...
Dimo558 Dimo558  08.06.2020 02:27
1. Ребро куба 4см. Найти площадь полной поверхности. 2. Решить неравенство: log2(2x - 6) log24 3. Решить неравенство: 4. Решить уравнение: - 2cosx = 0 5. Вычислить: lg13 – lg130...
2003247 2003247  08.06.2020 02:28
Прямой треугольник с a = 3 см и tg b = 2 верху 3. Найдите b, c, h и S!...
sanyaleleckov sanyaleleckov  08.06.2020 02:28
Требуется найти общее решение системы дифференциальныхуравнений методом исключения....
lsodh lsodh  08.06.2020 02:28
В группі 12 хлопців і 15 дівчат . Треба обрати делегацію з 2 студентів для участі у студентській конференції. Яка ймовірність того,що будуть обрані а) два хлопці; б) дві дівчини...
24j18g81B 24j18g81B  08.06.2020 02:29
Пояснити виконання дій різними та обгрунтувати їх , спираючись на властивості дій : 72:24....

Популярные вопросы