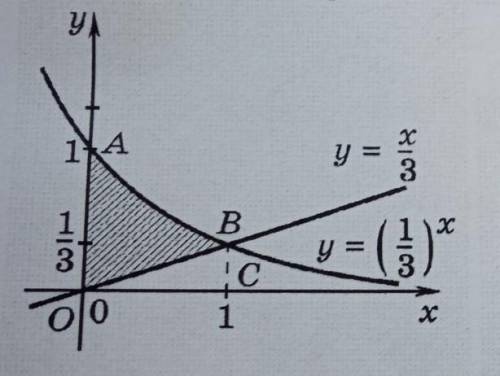
Запишите площадь заштрихованной фигуры с интеграла ​

вотт

Пошаговое объяснение:

Мы должны вычислить площадь заштрихованной фигуры. Для этого мы можем использовать интеграл.

Для начала давайте рассмотрим фигуру и разделим ее на две части: треугольник и прямоугольник. Для каждой из этих частей мы будем вычислять площади отдельно.

Начнем с треугольника. Мы знаем, что площадь треугольника равна половине произведения основания и высоты. В данном случае, основание треугольника равно 2 и высота равна 4. Таким образом, площадь треугольника равна (1/2) * 2 * 4 = 4.

Теперь перейдем к прямоугольнику. Мы можем использовать формулу для вычисления площади прямоугольника, которую мы знаем: длина * ширина. В данном случае, длина прямоугольника равна 4, а ширина равна 2. Таким образом, площадь прямоугольника равна 4 * 2 = 8.

Теперь мы можем сложить площади треугольника и прямоугольника, чтобы получить общую площадь заштрихованной фигуры. 4 + 8 = 12.

Итак, площадь заштрихованной фигуры равна 12.

Мы использовали простые формулы для вычисления площади треугольника и прямоугольника. Это позволяет нам разделить сложную фигуру на более простые части и вычислить их площади отдельно. Затем мы суммируем эти площади, чтобы получить полную площадь фигуры.

Мы также могли бы использовать интеграл для вычисления площади фигуры. В данном случае, мы должны были бы разбить фигуру на элементарные области и интегрировать их площади отдельно. Это более сложный метод, который требует знания математического анализа и интегрирования. Но в данном примере мы использовали более простой подход с использованием базовых формул для площади треугольника и прямоугольника.

Надеюсь, эта информация позволила вам понять, как вычислить площадь заштрихованной фигуры с использованием интеграла или базовых формул. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их.