Запишите множество корней уравнения1) x(x-1)=0; 2) (x-2)(x²-4)=0; 3) x=2 4) x²+3=0
Другие вопросы по теме Математика
Популярные вопросы
- Какие вам известны виды движения вод мирового океана? Как изображается...
1 - Для наведеного переліку речовин укажіть назви, до якого класу речовин...
1 - Доя острого угла а найдите sina, tga, ctg a, если соsа очень надо...
1 - В предложениях подчеркни главные и второстепенные члены предложения....
3 - Белгісіз санды 9-ға бөлгенде ,86 сан шықты және 5 қалдық қалды .Бөлгішті...
1 - Седьмое задание complete these...
3 - Дан прямоугольный треугольник АВС , с прямым угло С. Найдите угол А,...
1 - Как из дельта(a*b) сделать дельта a* дельта b...
1 - Что такое диффузия? Как можно увеличить скорость диффузии? Быстро...
1 - Виберіть правильне твердження: Виберіть одну відповідь: Анди є частиною...
1
1).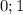
2).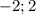
3).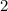
4).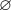
При решении будем пользоваться тем, что если произведение двух (или более) чисел равно нолю, то хотя бы одно из них равно нолю.
1).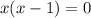
То есть, либо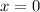 , либо
, либо 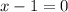
2).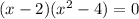
Получаем, либо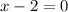 , либо
, либо 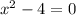
3).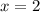
Здесь без комментариев, уравнение уже решено.
4).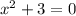
Переносим тройку вправо: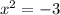 .
.
А так как в действительных числах квадрат числа не может быть отрицательным, то и уравнение корней не имеет.