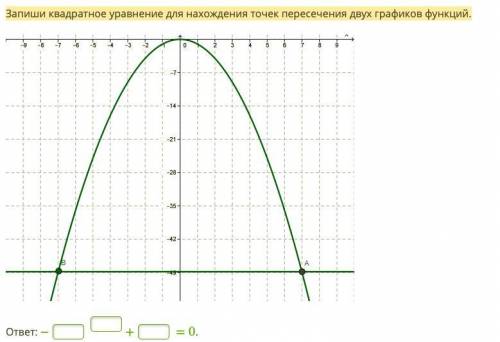
Запиши квадратное уравнение для нахождения точек пересечения двух графиков функций.

Чтобы записать квадратное уравнение для нахождения точек пересечения двух графиков функций, мы должны сначала определить функции, представленные на графике.

На данном графике у нас две функции: одна функция представлена синим цветом, другая функция — красным цветом. Давайте обозначим синюю функцию как f(x) и красную функцию как g(x).

На графике мы видим, что эти две функции пересекаются в двух точках. Мы можем обозначить эти точки пересечения как (x1, y1) и (x2, y2).

Чтобы записать квадратное уравнение для нахождения точек пересечения, мы можем приравнять эти две функции. То есть, уравнение будет выглядеть следующим образом:

f(x) = g(x)

Теперь давайте рассмотрим оба графика отдельно и найдем функции, которые они представляют.

На синем графике мы видим параболу в форме буквы "U". При этом вершина параболы находится в точке с координатами (h, k), где h — это горизонтальный сдвиг параболы, а k — вертикальный сдвиг параболы. Это означает, что функция f(x) будет иметь следующий вид:

f(x) = a(x-h)^2 + k

где a — коэффициент, определяющий степень "открытости" параболы. Если a положителен, парабола будет направлена вверх, если отрицателен — вниз.

Теперь рассмотрим красный график. Мы видим прямую линию, которая проходит через точку (p, q) и имеет наклон k. Это означает, что функция g(x) будет представлена в следующем виде:

g(x) = m(x - p) + q

где m — это коэффициент наклона прямой. Он определяет, как быстро прямая поднимается или опускается.

Теперь, когда мы знаем формулы для обоих функций, мы можем записать уравнение для точек пересечения, приравняв функции f(x) и g(x):

a(x-h)^2 + k = m(x - p) + q

Далее, чтобы решить это уравнение и найти значения x1 и x2, мы должны упростить уравнение, раскрыть скобки и привести подобные члены в квадратном уравнении. После этого полученное квадратное уравнение можно решить с помощью различных методов, например, метода завершения квадрата или квадратного корня.

Таким образом, квадратное уравнение для нахождения точек пересечения двух графиков функций будет выглядеть следующим образом:

a(x-h)^2 + k = m(x - p) + q