Запишіть рівняння дотичної та нормалі до кривої у=f(x) y точці К(х0,у0)

Ответы

kstarikova1 06.07.2022 09:35

Написать уравнение касательной и нормали к графику функции f(x)=x^4/4-27x+60 в точке х₀=2.

ответ:

Уравнение касательной имеет вид y=48-19x.

Уравнение нормали имеет вид y=188/19+х/19.

Пошаговое объяснение:

Вспомним общий вид уравнения касательной:

$\Large \boldsymbol {} \text{ $ \boldsymbol{\sf \star \ y=f(x_0)+f'(x_0)(x-x_0)}$ \boldsymbol}$

И общий вид уравнения нормали:

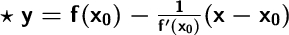
$\Large \boldsymbol {} \text{ $ \boldsymbol{\sf \star \ y=f(x_0)-\frac{1}{f'(x_0)}(x-x_0)}$ \boldsymbol}$

1. Найдём f(x₀).

Для этого в функцию вместо переменной х подставляем значение х₀=2.

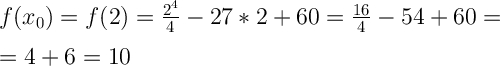
$\Large \boldsymbol {} f(x_0)=f(2)=\frac{2^4}{4}-27*2+60=\frac{16}{4} -54+60==4+6=10$

2. Найдём производную функции.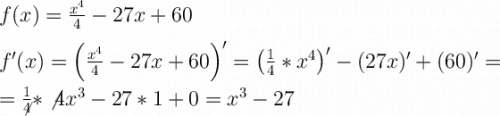

$\Large \boldsymbol {} f(x)=\frac{x^4}{4}-27x+60f'(x)=\left(\frac{x^4}{4}-27x+60\right)'=\left(\frac{1}{4}*x^4\right)'-(27x)'+(60)'==\frac{1}{\not4}*\not4x^3-27*1+0=x^3-27$

3. Найдём f'(x₀).

Для этого в производную функции вместо переменной х подставляем значение х₀=2.

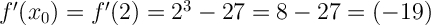
$\Large \boldsymbol {} f'(x_0)=f'(2)=2^3-27=8-27=(-19)$

4. Записываем уравнение касательной.

Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения касательной.

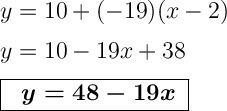
$\Large \boldsymbol {} y=10+(-19)(x-2)y=10-19x+38boxed{ \text{ $ \boldsymbol{ \ y=48-19x}$ \boldsymbol}}$

5. Записываем уравнение нормали.

Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения нормали.

$\Large \boldsymbol {} y=10-\frac{1}{-19} (x-2)y=10+\frac{x}{19} -\frac{2}{19}y=9\frac{17}{19} +\frac{x}{19} }boxed{ \text{ $ \boldsymbol{ \ y=\frac{188}{19} +\frac{x}{19} }$ \boldsymbol}}$