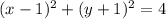Записати рівняння кола , центр якого знаходиться в точці с(1; -1) і пряма 5х-12у+9=0 є дотичною кола.
Другие вопросы по теме Математика
Популярные вопросы
- Какое средство выразительности употреблено в этой строчке туча кружево в роще...
2 - Напишите небольшие стишки на тему омонимы...
3 - Луч ор делит угол угол аов, равный 150градусов, на два угла так , что 2уголаор=3...
3 - Подалейста 10 примеры всех словообразования прилагательных!...
3 - Синтаксический разбор : новый год наступил в нашей /нн)ой россии и получив...
1 - Прочитайте текст. ответьте сложными предложениями на вопросы. находчивая лиса....
1 - Вшколе 500 учеников, среди них 265 девочек (девочки). сколько процентов учащихся...
2 - Опишите, что вы видите утром (вечером,ночью,днем) из окна вашего дома (класса)....
3 - Выпиши слова в таком порядке: 1) со значением приближения 2) со значением нахождения...
2 - Уфлоксов белая окраска и плоская форма венчиков доминирует над кремовой окраской...
2
Пусть уравнение окружности имеет вид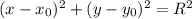 , по условию, центр окружности имеет координаты (1;-1), подставляем
, по условию, центр окружности имеет координаты (1;-1), подставляем
Из уравнения прямой получим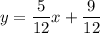 .
.
Подставляем в уравнение (1), получим
Прямая 5x - 12 y + 9 = 0 и окружность имеют одну общую точку. Поэтому дискриминант последнего квадратного уравнения нужно приравнять к нулю (имеет один корень).
Отрицательное значение R = -2 нам не нужен. Подходит R = 2.
Искомое уравнение окружности: