Записать матрицу A размерности m×n, используя заданную формулу
вычисления ее элементов.
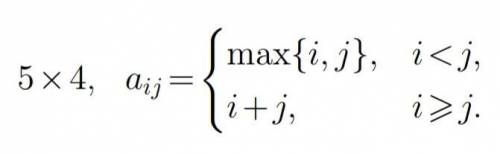
Другие вопросы по теме Математика
Популярные вопросы
- Єзавдання виписати 2 складних реченяня...
2 - Скем поведешься от того и наберешься. о чем хотел нам сказать автор?...
3 - Сколько процентов составляет число 17 от 50? 10...
2 - Составь и запиши вопросы о том, о чем тебе хотелось бы узнать на...
1 - Для чего бухгалтерам нужен компьютер? !...
2 - Системное уравнение {x+y=-5 {3x-y=-7...
1 - Длина прямоугольника равна 86 см, а ширина на 18 см меньше. какого...
2 - :4арип,5дыбыстан туратын соз,2арип,3дыбыстан туратын соз,5арип,4дибистан...
1 - Ломонная состоит из 2 звеньев.длина первой 1 дц,длина второй на...
2 - Как меняется море в сказке о рыбаке и рыбке рисунок...
2
Чтобы записать матрицу A размерности m×n с использованием заданной формулы вычисления ее элементов, следуйте следующим шагам:
1. Вначале, определите размерности матрицы, то есть значения m и n. Обычно это указывается в условии задачи.
2. Создайте пустую матрицу A размерности m×n. Например, если m=3 и n=4, то матрица будет выглядеть следующим образом:
A = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
3. Для каждого элемента матрицы A[i][j], где i - номер строки, j - номер столбца, используйте заданную формулу для вычисления значения элемента. В данном случае формула выглядит следующим образом: A[i][j] = i^2 - j^3.
4. Запишите полученное значение в соответствующий элемент матрицы A.
Давайте рассмотрим пример. Предположим, что m=3 и n=4. Следуя шагам из предыдущего пункта, начнем вычислять элементы матрицы A:
A[0][0] = 0^2 - 0^3 = 0 - 0 = 0
A[0][1] = 0^2 - 1^3 = 0 - 1 = -1
A[0][2] = 0^2 - 2^3 = 0 - 8 = -8
A[0][3] = 0^2 - 3^3 = 0 - 27 = -27
A[1][0] = 1^2 - 0^3 = 1 - 0 = 1
A[1][1] = 1^2 - 1^3 = 1 - 1 = 0
A[1][2] = 1^2 - 2^3 = 1 - 8 = -7
A[1][3] = 1^2 - 3^3 = 1 - 27 = -26
A[2][0] = 2^2 - 0^3 = 4 - 0 = 4
A[2][1] = 2^2 - 1^3 = 4 - 1 = 3
A[2][2] = 2^2 - 2^3 = 4 - 8 = -4
A[2][3] = 2^2 - 3^3 = 4 - 27 = -23
Таким образом, получаем матрицу A размерности 3×4:
A = [[0, -1, -8, -27],
[1, 0, -7, -26],
[4, 3, -4, -23]]
Обратите внимание, что в формуле использовались операции возведения в степень (i^2 - j^3), а также операции вычитания для вычисления значения элемента A[i][j].
Надеюсь, данное объяснение позволяет вам лучше понять, как записывать матрицу A с использованием заданной формулы вычисления элементов. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их.