Задумано двузначное число меньшее 70. Также известно, что оно на 26 больше произведения своих цифр. Какое число задумано? Решите , буду благодарен)
Другие вопросы по теме Математика
Популярные вопросы
- Убабушки 20 чашек: 2 с красными цветами, остальные с синими. бабушка...
3 - Какая точка соответствует числу √65...
2 - Составить связанные предложения лекарственные растения волгоградской...
2 - 1.почему необходима классификация растений? 2.какие единицы систематики...
1 - Сторона параллелограмма равна 4.5 , высота, проведенная и этой стороне...
1 - (4 5/12-3 7/18) /9,25+5/6 (0,4+1/8+0,75)*2/3 если можно с решением.заранее...
1 - Какя точка соответствует числу √65?...
1 - Спереводом прочитайте текст и сделайте перевод на язык. a trip to...
3 - Замени данные словосочетания глаголами с суффиксами -ова-(ева) и...
2 - Разберите слово беготня по составу! )...
2
Задумано число 32 или 56.
Пошаговое объяснение:
Пусть задумано число Тогда по условию
Тогда по условию
Так как по условию задачи число меньше 70, то его первая цифра меньше 7, значит
Поскольку цифра,
цифра,  и на это выражение можно умножить обе части неравенства.
и на это выражение можно умножить обе части неравенства.
То есть «кандидаты» в должны, с одной стороны, быть из диапазона от 1 до 7, а с другой число
должны, с одной стороны, быть из диапазона от 1 до 7, а с другой число  должно быть целым. Перебором убеждаемся, что подходят
должно быть целым. Перебором убеждаемся, что подходят  или
или 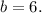 Тогда
Тогда
Искомые числа — 32 или 56.