Задание по математическому анализу прикреплено ниже
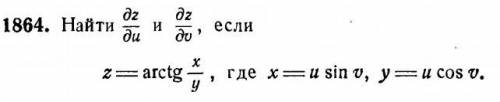
Другие вопросы по теме Математика
Популярные вопросы
- Символом чего является пряник в повести А.С.Тютчева Муму...
3 - Отнимите 2 2/5 - 16 целых 2/3...
1 - У відрі поміщається 10 літрів води .скільки склянок води у відрі...
3 - Рассчитайте массу оксида серы 4 который образуется при взаимодействии 350 г серы...
3 - Write letter about concert 120-150 words...
2 - Функция нескольких переменных. Решите эти задания!...
3 - Росуждение какие поступки человек делает больше ...
1 - Решите уравнение,8 класс4x^2+1=0...
2 - Вместо звёздочки поставьте цифры так чтобы сложение вычитание было выполнено верно...
2 - Укажите хронологические рамки колонизации территории Казахстана...
2
Формулы:
(везде закругленная d)
Собираем:
первая:
вторая: