Задание: найти производную(фото прилагается). Заранее
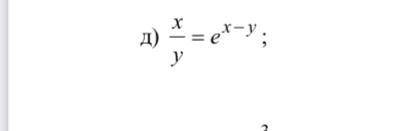
Другие вопросы по теме Математика
Популярные вопросы
- Какое жилкование у подорожника, хвоща полевого, кизила обыкновенного и у семейства...
3 - Решить примеры по действиям в ! 1)90*(25 338 : 6)-379= 2) (130 *80 - 1805): 3=...
2 - Вычисли умножение 495*142 262*360 153*402 320*450 332*240 452*202 394*125 170*640...
2 - Определить типы реакций. 1) с2h5oh = c2h4 + h2o 2) 2nh4cl + ca(oh)2 = cacl + 2h2o...
1 - Разгадайте загадку: в автобусе ехало 4 подростка, у каждого подростка в сумке по...
1 - А.)назовите 4 цветных моря и расположи эти названия в алфавитном порядке.в.)почти...
1 - Скаждым данным именем собственным составьте предложение официально-делового стиля,...
3 - Одна вторая одного месяца, это сколько?...
1 - Сочинение на тему школа моей мечты я учусь в 20 школе имени фёдора попова г. якутска....
3 - 1) 5x²-14x+8=0 2) 3x²-10x+7=0 3) 9x²-12x+4=0 4) -4x²-12x+7=0 с решением и как можно...
1
Пошаговое объяснение: