Задание: Найти предел не используя правило Лопиталя.
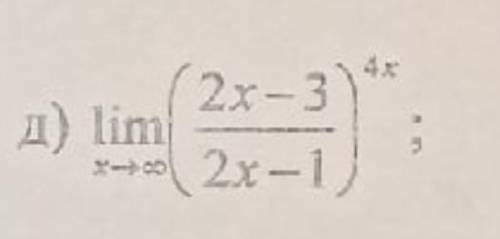
Другие вопросы по теме Математика
Популярные вопросы
- Зарубіжна література описати питаня ...
2 - Чому вчить нас повість І Гавроша неймовірні пригоди Івана сила ...
1 - Сіз отбасыңызбен саяхатқа шықтыңыз. Саяхатыңызды сипаттап,суреттеп жазыңыз. (50-60...
1 - Решить задачи с 1.30 - 1.35...
1 - Заполните таблицу проблемы связаны с освоением природных ресурсов без фигни ...
2 - Ұлы дала түрғындарының әскери өнері туралы берілген сұрақтарға жауап беріңіз...
1 - Закінчити рівняння реакцій Cu(OH)2 =H2S2O3 =2к+2H2OZn +2HCl =FeCl3+3NaOH = ...
1 - Write about your fWrite about your favourite city in the world. Write full answers...
2 - решить Одна сторона прямоугольника 1 дм,это на 9 см больше его другой стороны...
2 - 7. Развернутый угол Амс разделен лучом МК на два угла АМК и кмс. Найдите градусную...
3
ответ: e^(-4).
Пошаговое объяснение:
Так как (2*x-3)/(2*x-1)=1-2/(2*x-1), то данное выражение можно представить в виде [1-2/(2*x-1)]^4*x. Положим -2/(2*x-1)=t ⇒4*x=2-4/t и при x⇒∞ t⇒0. Тогда данное выражение примет вид: (1+t)^(2-4/t)=[(1+t)^2]/[(1+t)^(4/t)]. Так как предел числителя при t⇒0 равен 1, то искомый предел равен пределу выражения 1/[(1+t)^(4/t)]=1/[(1+t)^(1/t)]^4. И так как при t⇒0 предел в скобках [ ] есть ни что иное, как второй замечательный предел, равный e, то искомый предел равен 1/e^4=e^(-4).