ЗАДАНИЕ НА Задание = тема. В каждой теме 2 задания. Есть ответы в большинстве задач, нужно решение. Задание 1
• Телефонный номер состоит из 6 цифр (первая не равна нулю). Какова вероятность того, что все цифры четные? ответ: 0,0139.
• Рисунок на белой ткани представляет собой окрашенные горошины радиусом в 2 см, которых в среднем 25 шт. на 1 кв. м. Какова вероятность того, что при случайном проколе игла попадет: а) в круг; б) вне круга? ответ: а) 0,031; б) 0,969.
Задание 2
• Вероятность выбить 10 очков на данной дистанции для данного стрелка при одном выстреле равна 0,1; девять очков – 0,3. Какова вероятностью того, что при одном выстреле будет выбито не менее девяти очков? ответ: 0,4.
• Определить вероятность безотказной работы одного из пяти дублирующих одинаковых, независимо работающих устройств, если они обеспечивают безотказную работу системы с надежностью (вероятностью) 0,99968. Система работает, если работает хотя бы одно из дублирующих устройств. ответ: 0,8.
Задание 3
• Что вероятнее: а) выиграть у равносильного противника три партии из четырех или пять из восьми: б) не менее трех партий из четырех или не менее пяти из восьми: ответ: а) три из четырех партий; б) не менее пяти из восьми.
• Вероятность появления события А при каждом испытании равна 0,7. Сколько раз достаточно повторить испытание, чтобы с вероятностью 0,9 можно было утверждать, что относительная частота появления события А отклонится от вероятности события А не более, чем на 0,05? ответ: не менее 228 раз.
Задание 4
• Найти закон распределения и функцию распределения количества выходов из строя трех независимо работающих станков, если вероятность выхода из строя для каждого станка 0,2. Определить среднее число простаивающих станков. ответ:
1) Х 0 1 2 3
Р(Х) 0,512 0,384 0,096 0,008
• Механизм в процессе работы в течение часа испытывает в среднем 60 толчков. Какова вероятность того, что за 30 сек. не будет ни одного толчка? ответ: 0,61.
Задание 5
• Поезда метро идут равномерно с интервалом в 4 мин. Какова вероятность того, что пассажир, пришедший на платформу в определенный момент времени, появился не ранее, чем за две минуты после ухода поезда, но не позднее, чем за минуту до отхода следующего поезда метро? ответ: 0,25.
• Случайная величина задана функцией распределения
Функция прикреплена во вложении.
Найти дисперсию случайной величины. ответ: D(X)=3.
Задание 6
• Если отклонение размера от номинала менее 0,345 мм, ему присваивают знак качества. Систематические отклонения исключены, а случайные подчинены нормальному закону со средним квадратичным отклонением 0,3. Каково среднее число изделий со знаком качества в партии из 100 изделий? ответ. 75.
• Рост взрослых женщин в однородной группе является случайной величиной, распределенной нормальному закону с математическим ожиданием 164 см и средним квадртичным отклонением 5,5 см. Найти вероятность того, что ни одна из пяти наудачу выбранных женщин не будет иметь рост более 160 см. ответ: 0,0007.
Задание 7
• При проверке 29 пар обуви было обнаружено, что 3 должны быть уценены из-за дефектов фурнитуры. Оценить вероятность уценки изделий и найти точность оценки с надежностью γ =0,05.
• Проводились взвешивания комплексной нити. Результаты измерений массы M (г): 22,5; 23,5; 23,2; 21,4; 22,8; 23,1. Найти оценки математического ожидания и дисперсии.
Задание 8
• В таблице приведены измерения длины ворсинок пряжи. Х- длина ворсинки в миллиметрах, ni – число ворсинок длины xo
X 0,5 0,7 1,0 1,2 1,5
ni 8 15 12 10 5
• Проверить гипотезу Н0: длина ворсинок подчиняется нормальному закону. Уровень значимости 0,05.
Задание 9
• Для исследования системы случайных величин (X,Y) произведена выборка объема n=10 (-1,1); (-1,0); (0,-1); (0,2); (0,0); (1,-1); (1,1); (-1,-1); (0,0); (-1,0)
• Найти оценку коэффициента корреляции и проверить его значимость при уровне значимости α=0,05. Написать выборочное уравнение линейной регрессии.
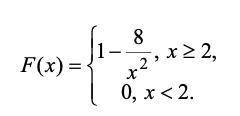
Ответы
Показать ответы (3)
Другие вопросы по теме Математика
Популярные вопросы
- Как называеться-особи у каторых олельные гены одинаковы называеться? заранее...
3 - Периметр прямоугольника равен 22см, его ширина b см.вычеслите площадь прямоугольника,если...
2 - Мечты захара беркута про будущую жизнь...
1 - Вшкольной олимпиаде по участвовало на 13 человек больше чем в олимпиаде...
2 - (5+а+б) а + б нужно написать допустимые значения....
3 - Составить схемы предложений мама испекла пиорг...
2 - Верно ли высказывание 8 класс тело обладает положительным зарядом в том...
1 - Выпивать мероприятия правления дария первый...
2 - Прощайте все.я удаляю приложение. последний вопрос. эссе 120 слов на любую...
2 - Решить уравнение. 24^2*х+17*х-14^2*х-500=17408/16 ^-это степень. 24 во...
1