Задание на фото!
Найти частное решение уравнения с разделяющимися переменными.
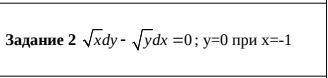
Другие вопросы по теме Математика
Популярные вопросы
- ответьте на вопросы,которые идут к тексту ниже : 1) формулировка проблем исходного...
3 - 1. собрались старые зайцы, сбежались маленькие зайчата, выпишите глаголы. выделите...
1 - Яким став сашко смик в кінці твору таємне товариство боягузів...
3 - Цитатный план рассказа м.москва. зощенко обезьяний язык ....
1 - Кданным словам подбери однокоренные слова выдели корень. скворец, летел, дело,...
2 - Мне нужно на языке буквами стих this is my house it s number tmo there s a bedroom,...
2 - 5) клиент положил в банк а рублей. какая сумма будет на его счете через 1 год,...
2 - 1.найти корни уравнения (3x-1)(4-x в квадрате)=0, принадлещие примежутку [-4;...
3 - Как зделать барыс септк по казазкаму...
2 - 6) население города составляет сейчас а тысяч жителей и увеличивается ежегодно...
1
ответ: y=(√x-i)², где i=√(-1).
Пошаговое объяснение:
Разделив уравнение на произведение √x*√y, получаем dy/√y-dx/√x=0. Интегрируя, находим 2*√y-2*√x=2*C, где C - произвольная постоянная. Отсюда √y=√x+C и y=(√x+С)². Используя условие y(-1)=0, получаем уравнение 0=(√(-1)+С)², откуда C=-√(-1)=-i. Тогда y=(√x-i)².