Задание из высшей математики. Вычислите пределы
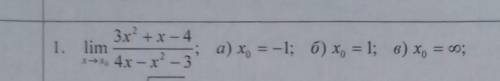
Другие вопросы по теме Математика
Популярные вопросы
- Сколько различных пятизначных чисел можно составить с цифр 34567 если...
3 - Выпишите грамматические основы из предложений еще ударяли холодные...
2 - (35 б. ) 7 класс. тема : взаимосвязь компонентов биоценоза и их при...
1 - Приключение капитана врунгеля составить 10 вопросов 9 - 12 главы !...
2 - Как изменились быт условия труда и жизни в 50-60-е гг в странах запада...
1 - 180 граммах воды растворили 20 граммов хлорида калия определите массовую...
3 - Синтаксический разбор предложения из художественной ....
3 - Причина ослабления тюргешского каганата...
1 - Сочинение на тему мое любимое произведение и быстро 10 б...
1 - Запиши, при каком значении x выражение 21010 - x принимает наименьшее...
2
(см. объяснение)
Пошаговое объяснение: