ЗАДАНИЕ 7! диагонали правильного шестиугольника ABCDEF пересекаются в точке О. Укажите вектор, равный вектору 1/2AD - 1/2CF + 1/2BE, началом и концом которого являются вершины этого шестиугольника. (рис. 3.6.)

Пошаговое объяснение:

прежде всего определимся с нашими половинами векторов.

определение:

Произведением вектора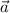 на число k называется вектор, получающийся из вектора 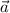растяжением (при k > 1) или сжатием (при k <1 ) в k раз, причём направление вектора 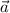сохраняется, если k >0  , и меняется на противоположное, если k <0 .

Итак наши вектора

Теперь будем вычитать

,

а теперь складывать.

Перенесем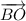  параллельно до точки начала 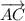и по правилу параллелограмма получим результат

ответ