1. Математика
  2. Задание 5. Решите систему

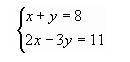
Задание 5. Решите систему линейных уравнений методом Крамера


Задание 5. Решите систему линейных уравнений методом Крамера

yuliyabondar2 yuliyabondar2    1   08.01.2021 17:03    1

Ответы
dasha685331 dasha685331  07.02.2021 17:04

(7; 1)

Пошаговое объяснение:

Запишем и вычислим главный определитель системы.

Элементами главного определителя являются коэффициенты при переменных "х" и "у":

\Delta = \left|\begin{array}{cc}1&1\\2&-3\end{array}\right| = 1 \cdot (-3)-1 \cdot 2=-3-2=-5 \neq 0;

Главный определитель не равен нулю ⇒ система совместна.

Запишем и вычислим первый вс определитель. Для этого  заменим первый столбец на столбец свободных членов:

\Delta_{x}=\left|\begin{array}{cc}8&1\\11&-3\end{array}\right| =8 \cdot (-3)-11 \cdot 1=-24-11=-35;

Запишем и вычислим второй вс определитель. Для этого  заменим второй столбец на столбец свободных членов:

\Delta_{y}=\left|\begin{array}{cc}1&8\\2&11\end{array}\right| =1 \cdot 11-2 \cdot 8=11-16=-5;

Переменные "х" и "у" находятся по следующей формуле:

x=\frac{\Delta_{x}}{\Delta}, \quad y=\frac{\Delta_{y}}{\Delta};

x=\frac{-35}{-5}=7, \quad y=\frac{-5}{-5}=1;

x=7, \quad y=1;

(7; 1);

ПОКАЗАТЬ ОТВЕТЫ
Mariapolitova Mariapolitova  07.02.2021 17:04

\left \{ {{x+y=8} \atop {2x-3y=11}} \right. = \left \{ {{x=8-y} \atop {2*(8-y)-3y=11}} \right. = 2*(8-y)-3y=11\\\\16-2y-3y=11\\-5y=11-16\\-5y=-5\\y=1\\\\x=8-y\\x=8-1\\x=7

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
huntress26 huntress26  08.05.2020 06:40
Вычисли площади фигур. Можно ли это сделать разными ЧЕРЕЗ 20 МИНУТ СДАВАТЬ...
alinkarazborova alinkarazborova  08.05.2020 06:41
X 2 − y 3 − 1 = 0 x 2 - y 3 - 1 = 0 x 5 − y 4 + 1 = 0 x 5 - y 4 + 1 = 0...
BackTiger007 BackTiger007  08.05.2020 06:41
с 1224, 1226, 1228 номерами...
TOPTopTOP1vvv TOPTopTOP1vvv  08.05.2020 06:41
На круговой диаграмме показано наличие книг в фонде некоторой библиотеки. Пользуясь диаграммой, ответьте на во Каких книг меньше всего в библиотеке? b) Половину фонда библиотеки...
Sofwork Sofwork  08.05.2020 06:41
7. В прямоугольный треугольник с гипоте нузой АС вписана окружность, касающа яся катета ВС в точке К. Известно, что BK = 13. Найдите радиус окружности....
ання2018 ання2018  08.05.2020 06:41
Родился малыш его ежемесячная прибавка в весе была различна при рождении он весил В 1 месяц 4,700 в 2 месяца 5,800 В 3 месяца 6,400 в 4 месяца 7 В 5 месяцев 7,400 в 6 месяцев...
linalimeofficip01ef8 linalimeofficip01ef8  08.05.2020 06:41
Решите уравнение. t:42,7=7,4:2,5​...
aav7 aav7  08.05.2020 06:41
Какие из пар чисел (5; – 1), (8; 3), (3; -8), являются решениями уравнения 7х – 2у = 37? хелп( У меня сор...
айка395 айка395  08.05.2020 06:41
Среднее арифметическое:Медиана:Мода:Размах:​...
abroe abroe  08.05.2020 06:41
Запиши уравнение к задаче, начало решения которой выглядит так: 1-я пачка 2-я пачка Было тетрадей 2x x Стало тетрадей 2x − 17 x+34 Известно, что количество тетрадей, получившихся...

Популярные вопросы