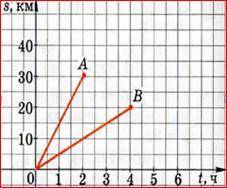
Задание 4. На рисунке построены графики движения пешехода (отрезок ОВ) и велосипедиста (отрезок ОА). С графиков ответьте на вопросы: 1) Какое время был в пути пешеход?
2) Какое время был в пути велосипедист?
3) Сравните двумя их скорости.
4) Какое расстояние между пунктами А и В?
Задание 6. Движение двух велосипедистов заданы функциями: S1=0,5t+3 и S2=1,25t
1) Постройте график зависимости пути от времени для обоих велосипедистов
2) По графику определите скорости обоих велосипедистов.
3) По графику определите через какое время они встретились.

20 км

Пошаговое объяснение:

Пункт А 2 часа со скоростью 30 км/час имеем 2*30=60км

Пункт Б 4 часа со коростью 20км/час

20*4=80км

Б-А=80-60=20км

Задание 4:

1) Чтобы определить время, в течение которого пешеход был в пути, нам необходимо проанализировать график его движения (отрезок ОВ). На графике видно, что пешеход начал свое движение в момент времени t=0 и закончил в момент времени t=10. Поэтому, время, в течение которого пешеход был в пути, составляет 10 единиц времени (можно измерять в секундах, минутах и т.д.).

2) Аналогично, чтобы определить время, в течение которого велосипедист был в пути, мы должны рассмотреть график его движения (отрезок ОА). На графике видно, что велосипедист начал движение в момент времени t=0 и закончил в момент времени t=8. Таким образом, время, в течение которого велосипедист был в пути, составляет 8 единиц времени.

3) Для сравнения скоростей пешехода и велосипедиста, мы можем обратить внимание на наклоны графиков их движения. Наклон графика пешехода (отрезок ОВ) является меньше, чем наклон графика велосипедиста (отрезок ОА). Как мы знаем, наклон графика показывает скорость, поэтому можно сделать вывод, что скорость велосипедиста больше, чем скорость пешехода.

4) Чтобы определить расстояние между пунктами А и В, нам нужно измерить горизонтальное расстояние между пересечением графиков ОА и ОВ. На графике видно, что это расстояние составляет около 8 единиц длины. В данном случае, можно измерять в метрах или любых других единицах длины.

Задание 6:

1) Чтобы построить графики зависимости пути от времени для обоих велосипедистов, мы должны использовать функции S1=0,5t+3 и S2=1,25t. Для этого возьмем различные значения времени t и подставим их в соответствующие функции, чтобы получить значения пути S1 и S2. Затем, построим точки на координатной плоскости, где по оси абсцисс будет время t, а по оси ординат - путь S1 и S2.

2) Чтобы определить скорость велосипедистов, мы должны рассмотреть наклоны их графиков зависимости пути от времени. Наклон графика S1=0,5t+3 равен 0,5, что означает, что скорость первого велосипедиста равна 0,5 единицы пути в единицу времени. Наклон графика S2=1,25t равен 1,25, что означает, что скорость второго велосипедиста равна 1,25 единицы пути в единицу времени.

3) Чтобы определить время встречи велосипедистов, мы должны найти точку пересечения их графиков. То есть, мы должны найти момент времени, когда значения пути S1 и S2 для обоих велосипедистов будут одинаковыми. Для этого приравниваем функции S1 и S2 друг к другу и решим полученное уравнение. Таким образом, мы найдем время, через которое они встретились.