Задание 2. Решите простейшие тригонометрические уравнения
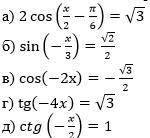
Другие вопросы по теме Математика
Популярные вопросы
- Используя метод электронного баланса, составьте уравнение реакции:...
1 - При сгорании 4,48 л (н.у.) газообразного органического вещества получили...
1 - Провели электролиз раствора хлорида натрия. К полученному раствору...
1 - Используя метод электронного баланса, составьте уравнение реакции:...
3 - Используя метод электронного баланса, составьте уравнение реакции:...
3 - Используя метод электронного баланса, составьте уравнение реакции:...
2 - Используя метод электронного баланса, составьте уравнение реакции:...
1 - Используя метод электронного баланса, составьте уравнение реакции:...
2 - Используя метод электронного баланса, составьте уравнение реакции:...
2 - Используя метод электронного баланса, составьте уравнение реакции:...
1
а)
n принадлежит Z.
б)
n принадлежит Z.
в)
n принадлежит Z.
г)
n принадлежит Z.
д)
n принадлежит Z.