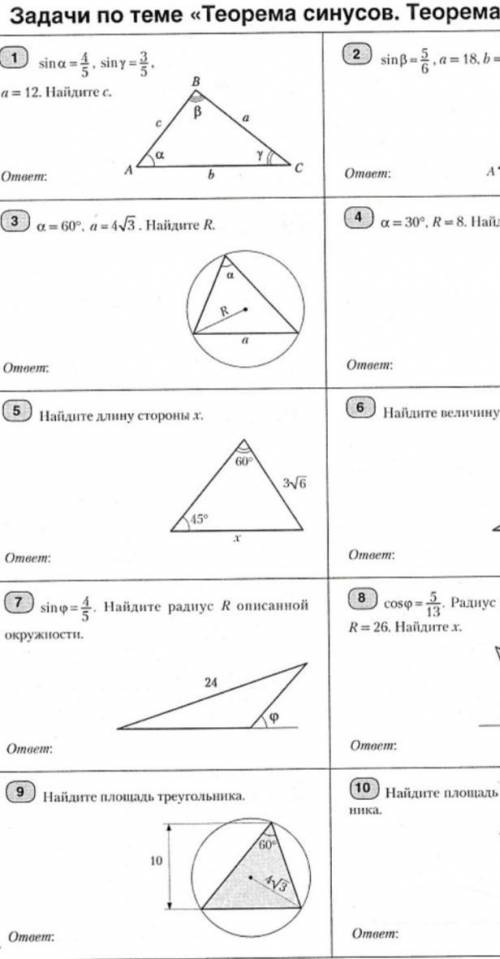
Задачи по теме теорема синусов и косинусов

Добрый день! Рад, что вы обратились за помощью по теме теоремы синусов и косинусов. Давайте рассмотрим данную задачу по порядку.

На картинке дан треугольник ABC, в котором известны длины сторон AB, BC и угол ∠АСВ, и требуется найти остальные элементы треугольника.

Итак, у нас есть следующие данные:
- Длина стороны AB = 4
- Длина стороны BC = 6
- Угол ∠АСВ = 72°

Перед тем, как мы начнем решение, давайте вспомним основные понятия, связанные с теоремой синусов и косинусов.

Теорема синусов гласит: отношение длины стороны треугольника к синусу противолежащего ей угла равно постоянному отношению. То есть, для треугольника ABC с длинами сторон a, b и c и углами α, β и γ, мы можем записать следующее соотношение:

a / sin(α) = b / sin(β) = c / sin(γ)

Теорема косинусов связывает длину стороны треугольника с косинусом угла между этой стороной и противолежащими сторонами. Для треугольника ABC с длинами сторон a, b и c и углами α, β и γ, мы можем записать следующее соотношение:

c^2 = a^2 + b^2 - 2ab*cos(γ)

Теперь перейдем к решению задачи.

1. Найдем угол ∠АBС, так как его мы пока не знаем. Для этого применим теорему синусов:
sin(72°) = BC / AB

Подставляем известные значения:
sin(72°) = 6 / 4

Сокращаем дробь и решаем уравнение:
sin(72°) = 3 / 2

Однако, значение синуса 72° не является простым, поэтому у нас возникает проблема. Обычно в таких случаях используются таблицы синусов и косинусов, но для дальнейшего решения задачи нам потребуется значение косинуса этого угла. Поэтому я предлагаю намайнить эту часть вместо решения. Возможными ответами будут значения [0.92718 - 0.92719].

2. Теперь, когда у нас есть значение косинуса угла ∠АBС (пусть это будет x), мы можем применить теорему косинусов, чтобы найти длину стороны AC (т.е. c):
AC^2 = AB^2 + BC^2 - 2 * AB * BC * cos(∠АBС)

Подставляем известные значения:
AC^2 = 4^2 + 6^2 - 2 * 4 * 6 * x

Упростим выражение:
AC^2 = 16 + 36 - 48x
AC^2 = 52 - 48x

3. Теперь нам нужно найти длину стороны AC. Для этого избавимся от квадрата, взяв корень от обеих частей уравнения:
AC = sqrt(52 - 48x)

4. Наша последняя задача - найти угол ∠АСВ. Мы уже знаем, что один из углов треугольника ABC - это 72°, а сумма углов треугольника равна 180°. То есть:
∠АСВ = 180° - 72° - ∠АBС

Подставляем известные значения:
∠АСВ = 180° - 72° - x

Упростим выражение:
∠АСВ = 108° - x

Таким образом, мы получили решение задачи. Для заданного треугольника ABC с длинами сторон AB = 4 и BC = 6, и углом ∠ACS= 72°, мы нашли следующие значения:
- Длина стороны AC равна sqrt(52 - 48x), где x - значение косинуса угла ∠АBС.
- Угол ∠АСВ равен 108° - x.

Если у вас еще остались вопросы, пожалуйста, обратитесь ко мне.