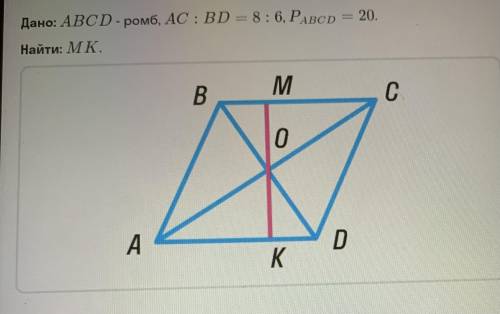
Задача во вложении………………….
Другие вопросы по теме Математика
Популярные вопросы
- Изопроцессы в газах. Газовые законы. Графическое представление....
1 - Задания 1. (а) Запишите изомеры С6Н10, содержащие кумулированную,...
2 - Это Химия только все надо задания...
1 - это соч по естествознанию...
1 - Выполните действия 5/21 + 2/3...
3 - ПОМГИТЕ АНГЛИЙСКИЙ ЯЗЫК СОЧЧ...
3 - Кыздергыштын жумыс температурасы 698C оны коршаган орта температурасы...
3 - ПАЖАЙЛУСТОЗадание 1. Выпиши из текста все предложения с обособленными...
3 - Деление обыкновенных дробей и смешанных чисел. Урок 4 Реши уравнения:...
3 - Дано: ∢1=137°,∢5=49°. Вычисли все углы.  Дано: ∢1=137°,∢5=49°. Вычисли...
1
S ромба = D • d / 2, где D и d диагонали (в нашем случае АВ и BD)
или
S ромба = a • h, где a - основание, h - диагональ ( в нашем случае h = МК; а = AD)
1) Р =4•AD
P = 20 (по условию)
Следовательно,
AD = Р : 4 = 20 : 4 = 5 - длина стороны ромба.
2) а = (√(D² + d²))/2,
где
а - сторона ромба
(в нашем случае а = AD = 5)
D и d диагонали (в нашем случае АВ и BD)
5 = (√(D² + d²))/2
√(D² + d²) = 10
D² + d² = 100
Но по условию:
АС:BD = 8:6, где D = AC; d = BD
Значит,
D = 8 • d / 6 = 4 • d / 3
Подставляем в уравнение:
D² + d² = 100
(4d/3)² + d² = 100
16d²/9 + d² = 100
9•16d²/9 + 9•d² = 9•100
16d² + 9•d² = 900
25d² = 900
900 - 25d² = 0
(30 - 5d) • (30 + 3d) = 0
1. 30 - 5d = 0
5d = 30
d = 30 : 5 = 6
2. 30 + 5d = 0
5d = -30
d = -30 : 6
d = -6 - не подходит
Значит, d = BD = 6
Тогда
D = АС = 4 • d / 3 = 4 • 6 / 3 = 8
4) S ромба = АС • BD / 2 - площадь ромба, где
S ромба = 8 • 6 / 2 = 48/2 = 24
С другой стороны
S ромба = AD • MK
где AD = 5
S ромба = 24
24 = 5 • МК
МК = 24 : 5 = 4,8
ответ: 4,8.