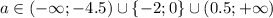Задача решить параметр. Я вроде как его решил, но не уверен в правильности решения поэтому как то так.

Другие вопросы по теме Математика
Популярные вопросы
- Сочинение на тему равнодушие или милосердие минимум 50 слов...
3 - The teacher is annoyed. We __ (not listen). What __ you __ (wait)...
3 - на стороні aс рівностороннього трикутника АВС взята точка М,а на продовженні...
1 - Упростить алгебраическую сумму многочленов...
3 - В параллелограмме MFKS MF относится к MK как 1:2 и угол SKM равен...
3 - 3. Що довідуємося зі свідчень Боплана про козацький табір як бойовий...
2 - File:///D:/Users/User/Downloads/IMG-a82e707d580df357c6096cf1d33388bd-V.jpg...
2 - Запасы воды Заполните пропуски в тексте. Многие государства Земли...
1 - 1. Найти область определения функции. 2. Выяснить, не является ли...
1 - Дано: АBCDА1B1C1D1 – куб, A1В1=5 см. Найти: 1) угол между A1С1 и BD;...
3
ответ: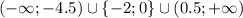
Пошаговое объяснение:
Если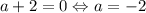
Уравнение имеет два решения, значит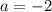 подходит
подходит
Если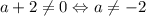 , то в совокупности два квадратных уравнения
, то в совокупности два квадратных уравнения
Тогда, либо их корни должны совпадать, что произойдет в случае, когда совпадают уравнения, т.е. при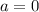 , убедимся, что корни есть
, убедимся, что корни есть 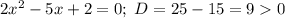
Либо одно из них имеет единственный корень, который совпадает с одним из двух корней другого, что невозможно, поскольку у этих уравнений совпадает сумма корней (по т. Виета она равна 5/(a+2))
Также подходят все значения параметра, при котором одно из них имеет 2 корня, а другое не имеет решений
Поскольку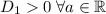 , то оно всегда имеет 2 корня, найдем при каких значениях параметра уравнение (2) не имеет корней
, то оно всегда имеет 2 корня, найдем при каких значениях параметра уравнение (2) не имеет корней
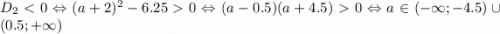
Итого получим, что уравнение имеет два решения при