Задача представлена на картинке

Пусть уравнение искомой кривой y=y(x). Рассмотрим произвольную точку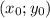 на плоскости,  производную в этой точке обозначим через 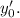Уравнение касательной к кривой будет иметь вид

Чтобы узнать, где эта касательная пересекается с осью OY, подставим x=0:

По условию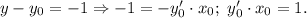

Поскольку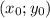 - произвольная точка, можно последнее условие переписать в виде

Поскольку по условию кривая проходит через точку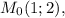 можем найти C:

И наконец, поскольку абсцисса точки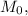 которая лежит на кривой, положительна, и во всех других точках кривой абсцисса будет положительной, поэтому окончательный ответ такой: