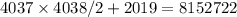Задача на комбинаторику, но точно не знаю, ответ отмечен, мне нужно решение)

Другие вопросы по теме Математика
Популярные вопросы
- Масса сушеного яблока состовляет 16% массы свежего яблока сколько кг свежих...
2 - Как правительство отреагировало на реформы Гайдая?...
1 - Как отличить в пробирках NaOH и Fe(OH)2, используя любые физические и химические...
1 - 16,45+16,6=?сколько будет?? ...
2 - В) среднее арифметическое 5,2 ; 7,2 ; 9,2...
1 - Тематичне оцінювання: Вторинний сектор господарства ІІ варіант І рівень ів (...
1 - Определи вид прилагательного:1. весенние грозы —относительноепритяжательноекачественное2....
2 - Семейство крестоцветные – это * Brassicáceae Rosaceae Brassicáles Rosáles...
3 - Распределите вещества по возрастанию основных свойств. NH3 , С3Н7NH2 , С6Н5NH2...
3 - Какие из названых здесь тел обладают потенциональной энергей: комнатная люстра,...
3
Числители образуют следующую последовательность: для соседних натуральных чисел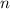 и
и 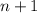 между ними выписываются натуральные от
между ними выписываются натуральные от  до
до  .
.
Для знаменателей наоборот: от до
до  .
.
Числители.
Рассмотрим множество номеров, под которыми стоит число 2020. Для этого разобьем числа на блоки. Длина каждого блока под номером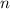 равна
равна 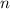 . Для всех блоков с номером
. Для всех блоков с номером 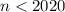 число 2020 появляться не будет. Начиная с
число 2020 появляться не будет. Начиная с 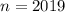 число 2020 будет в каждом блоке ровно 1 раз (числа в блоках различны). Первый раз число 2020 появится на
число 2020 будет в каждом блоке ровно 1 раз (числа в блоках различны). Первый раз число 2020 появится на 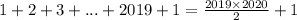 месте. Затем 2020 будет в каждом блоке
месте. Затем 2020 будет в каждом блоке 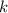 под номером
под номером 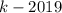 . Значит, множество мест числа 2020 задано последовательностью
. Значит, множество мест числа 2020 задано последовательностью 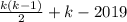 .
.
Знаменатели.
Число 2019 впервые появится в блоке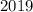 . Далее будет в каждом блоке под номером 2019. Значит, множество мест число 2019 задано последовательностью
. Далее будет в каждом блоке под номером 2019. Значит, множество мест число 2019 задано последовательностью 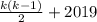 . Мы ищем число
. Мы ищем число 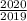 , поэтому
, поэтому 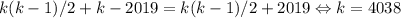 . Следовательно, это число будет стоят на месте под номером
. Следовательно, это число будет стоят на месте под номером