Задача дано: OA = 10, OB = 8 рис. Найти:
а)Координаты отрезка AB
б)Периметр треугольника MNP, где M, N, P - середины сторон треугольника OAB.
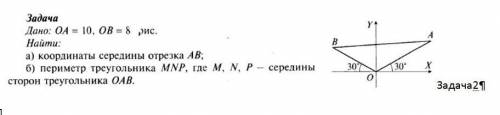
Другие вопросы по теме Математика
Популярные вопросы
- Өтінемін маған 948 есепті шығарып бересіздер ме...
1 - ПО ХИМИИ 1.Фосфорная кислота реагирует с веществами : H2SO4, KCL, NH3, Na20...
3 - При каких значениях переменной алгебраическая дробь x²+3x+1/x²-81 имеет смысл...
2 - Буду благодарна за ответ ...
3 - Анализи интерпретацииых слов по сказке Снегурочка» на 5словОбщий бал 20...
1 - 1. Вчера был дождь, но я ждал автобус. 2. У меня есть питомец, но он уже старенький....
3 - Прочитать текст и ответить на во Из Индии через Среднюю Азию и Казахстана в...
3 - Составить 10 предложений (5 - с определительными местоимениями, 5 - с указательными;...
2 - Спиши предложение раскрой скобки, вставь пропущенные буквы. (В)этом л...су...
2 - №1. Берілген сандар қатарының 27, 22, 25, 20, 22 арифметикалық ортасын, медианасын,...
2
ответ и Пошаговое объяснение:
Координаты точки А (10*sqrt(3)/2,10*1/2), так как координата по оси х
это величина ОА , умноженная на косинус 30 градусов, , а координата по оси у,это величина ОА , умноженная на синус 30 градусов.
Значит А(5*sqrt(3),5).
Точно также В(-4*sqrt(3),4).
Найдем длину АВ. Ее квадрат сумма квадратов разностей координат.(5*sqrt(3)+4*sqrt(3))^2+(5-4)^2=3*81+1=244
Значит длина АВ равна 2*sqrt(61)
Периметр АВС равен 8+10+2*sqrt(61)=18)+2*sqrt(61)
Периметр MNP, составленный из средних линий треугольника АВС равен
9+sqrt(61)
Здесь sqrt - корень квадратный, ^ - возведение в степень