Задача 6. (Сергей Костин) За три весенних месяца некоторого года понедельников было меньше, чем четвергов. Чего было меньше за три летних месяца того же года – вторников или пятниц?

Задача 7. (Григорий Гальперин)
Найдите все натуральные числа n, для которых n2 = n! + n. (Напомним, что n! – это произведение 1 · 2 · … · n первых n натуральных чисел.)

Задача 8. (Данила Иванов)
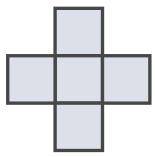
Два игрока играют в крестики-нолики на бесконечной клетчатой плоскости. Выигрывает тот, кто отметит пять клеток в виде креста (см. рисунок) своим значком. Всегда ли второй игрок может помешать первому выиграть?

Задача 9. (Михаил Евдокимов)
a) Можно ли все натуральные числа окрасить в три цвета так, чтобы каждый цвет присутствовал и произведение любых двух чисел одного цвета было числом того же цвета?
б) А в семь цветов?

Задача 10.
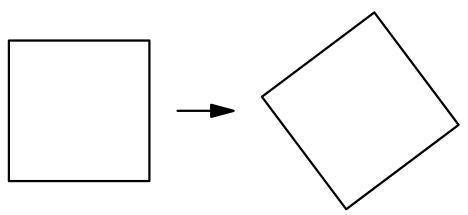
Придумайте разрезать квадрат на части и передвинуть их, не поворачивая, так чтобы получился такой же, но повёрнутый квадрат (например, как на рисунке).

sasha235sasha    3   03.11.2020 12:41    1