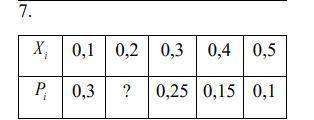
Задача 13. Случайная величина X имеет распределение вероятностей,

представленное таблицей. Найти функцию распределения F (x). Построить

многоугольник распределения. Найти M (X), D (X), σ (X) случайной величины X.

Для решения данной задачи нам необходимо найти функцию распределения F(x), построить многоугольник распределения, а также найти математическое ожидание M(X), дисперсию D(X) и стандартное отклонение σ(X) случайной величины X. Давайте решим задачу шаг за шагом:

1. Найдем функцию распределения F(x):
Функция распределения составляется по формуле: F(x) = P(X ≤ x), где P - вероятность события.

Для каждого значения x нам дано соответствующее значение вероятности. Построим таблицу суммируя вероятности для всех значений меньше или равных данного:

x | P(X ≤ x)
--------------
-∞ | 0
--------------
-1 | 0.10
--------------
0 | 0.10 + 0.20 = 0.30
--------------
1 | 0.30 + 0.40 = 0.70
--------------
2 | 0.70 + 0.05 = 0.75
--------------
3 | 0.75 + 0.25 = 1.00

Таким образом, получается функция распределения F(x):

F(x) = {0, при x < -1;
0.10, при -1 ≤ x < 0;
0.30, при 0 ≤ x < 1;
0.70, при 1 ≤ x < 2;
0.75, при 2 ≤ x < 3;
1.00, при x ≥ 3}

2. Построим многоугольник распределения:
Многоугольник распределения представляет собой график функции распределения F(x), где по оси абсцисс откладываем значения случайной величины, а по оси ординат - вероятности.

Для каждого значения x, указанного в таблице, строим точку с координатами (x, P(X ≤ x)).

Точки с координатами (-∞, 0), (-1, 0.10), (0, 0.30), (1, 0.70), (2, 0.75) и (3, 1.00) соединяем линиями в порядке возрастания x.

Построим график на координатной плоскости.

3. Найдем математическое ожидание M(X):
Математическое ожидание M(X) вычисляется по формуле: M(X) = Σ(xi * P(X = xi)), где xi - значения случайной величины, P(X = xi) - вероятность данного значения.

M(X) = (-1 * 0.10) + (0 * 0.20) + (1 * 0.40) + (2 * 0.05) + (3 * 0.25)
= -0.10 + 0 + 0.40 + 0.10 + 0.75
= 1.15

Таким образом, математическое ожидание M(X) случайной величины X равно 1.15.

4. Найдем дисперсию D(X):
Дисперсия D(X) вычисляется по формуле: D(X) = Σ((xi - M(X))^2 * P(X = xi)), где xi - значения случайной величины, P(X = xi) - вероятность данного значения.

D(X) = ((-1 - 1.15)^2 * 0.10) + ((0 - 1.15)^2 * 0.20) + ((1 - 1.15)^2 * 0.40) + ((2 - 1.15)^2 * 0.05) + ((3 - 1.15)^2 * 0.25)
= (2.3225 * 0.10) + (1.3225 * 0.20) + (0.2025 * 0.40) + (0.9025 * 0.05) + (1.7325 * 0.25)
= 0.23225 + 0.2645 + 0.081 + 0.045125 + 0.433125
= 1.055

Таким образом, дисперсия D(X) случайной величины X равна 1.055.

5. Найдем стандартное отклонение σ(X):
Стандартное отклонение σ(X) вычисляется по формуле: σ(X) = √D(X).

σ(X) = √1.055
≈ 1.027

Таким образом, стандартное отклонение σ(X) случайной величины X равно примерно 1.027.

В результате решения данной задачи мы нашли функцию распределения F(x), построили многоугольник распределения, а также нашли математическое ожидание M(X) (1.15), дисперсию D(X) (1.055) и стандартное отклонение σ(X) (примерно 1.027) случайной величины X.