За темою Диференціальні рівняння.
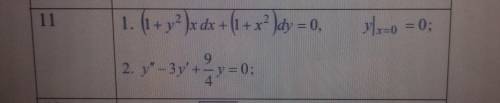
Другие вопросы по теме Математика
Популярные вопросы
- Тертя, це користь чи шкода для організму?...
2 - Груз массой 4 кг, закрепленный на пружине жесткостью 400 Н/м, совершает...
3 - История жизни Владимира Дубровского, по плану:1. Основная часть. История...
2 - Решите на скриншоте задание...
1 - перпендикулярні прямі AB i DC перетинаються в точці O. промінь OE проходить...
3 - 3.Як будуть йти промені після відбивання у вгнутому дзеркалі? Пояснити за...
3 - В правильной треугольной призме АВСА1В1С1 сторона основания равна 8 см,...
2 - Вычислите количество вещества, которое содержит 2,4•10 в 23 степени молекул...
1 - Найдите координаты середины отрезка АВ если А(5;-3);B(3;-7) с решением...
1 - Составить рассказ о революции во франции по алгоритму...
3
1.
Это ДУ с разделяющимися переменными
общее решение
частное решение
2. Это линейное однородное ДУ
общее решение