Является ли группой множество g(•)
r\{-1}; a•b=ab+a+b
Другие вопросы по теме Математика
Популярные вопросы
- От чего зависит климот в первую очередь...
1 - Help me please.Ex 3(beat or strike)...
1 - Здравствуйте, мне нужно нарисовать флаги в Word но у меня нет пк: Швеция, Тунис,...
2 - Все ли выгодно производить ? поясните свой ответ....
1 - Как влияют холодные океанические течения на климат Чили?...
3 - Потратили от 600 рублей сколько рублей потратили?...
3 - Определите вес, действующую на куб массой 6кг...
3 - Напишите , 5-7 предложений, как можно решить проблему кислотных дождей 1.2.3.4.5.6.7....
1 - Сөйлемдерді дұрыс құрастырып,жаз. 6 класс даю 15б...
2 - Complete the sentences with the words in the box. deer duck rabbit seal snow...
1
Заметим для начала, что операция коммутативна
Проверим, может ли при каких-то a и b из G получиться в результате операции число не из G (то есть -1, так как, очевидно, результат операции - действительное число)
То есть посредством операции нельзя выйти из R\{-1}
Найдем нейтральный элемент по этой операции:
Проверим свойство ассоциативности:
Посмотрим, у каждого ли есть обратный элемент. Рассмотрим произвольный элемент a:
Обратный существует (так как a не равен -1), а также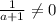 , то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
, то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
Таким образом, G - абелева группа.