Является ли данная функция = c1e3х + c1e^-2х решением
дифференциального уравнения у'' - y'-6у = 0
Другие вопросы по теме Математика
Популярные вопросы
- Терміново! ів! До іть, що знаєте...
1 - Расскажите о внутреннем строении лука...
1 - Подготовиться на черновиках к сочинению «Особенности русского характера»....
1 - Завершите мысли вокруг северного полюса солнце 6 месяцев не заходит в южном...
3 - покупатель купил крем для лица и шампунь рассмотри рисунок и ответь на вопросы....
2 - Почему одисей не называет цыклопу свое имя?...
3 - составить монолог 6-10 предложений....
3 - Решение и ответ на примера 432*724:432:724 Ровно...
1 - Для зниження кров яного тиску використовують розчинз масовою часткою магній...
3 - Велосипедист за 40мин проехал 10км.С какой скоростью он ехал?...
2
Найдём первую и вторую производную функции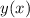 :
:
Подставим теперь данные выражения в дифференциальное уравнение:
Получили тождество, а значит, данная функция является общим решением дифф. уравнения.
P. S. На будущее: подстрочный индекс обозначается как a_n, надстрочный — как a^n. Если в индексе не одна буква/цифра, а несколько (в том числе и минус), то индекс берётся в скобки: