Який вираз має зміст при будь-якому значенні х? а)х-2/х2+9; б)х-2/х+9; в)х-2/х-9; г)х-2/х2-9

Ответы

ДимаМасленников 24.07.2020 13:41

Пошаговое объяснение:

Раціональній дріб буде мати зміст при умові , що знаменник не дорінює 0.

Визначимо , який вирах буде мати зміст ,для цього визначимо область допустимих значень (ОДЗ)

а)

х²+9≠0

х²≠-9

оскільки будь-яке число у квадраті буде додатнім , то ОДЗ (- ∞; +∞ ),

отже вираз буде мати зміст при будь-якому значенні , що відповідає умові.

б)

х+9≠0

х≠-9

ОДЗ (-∞ ; -9) ∪(-9;+∞),

що не відповідає умові

в)

х-9≠0

х≠9

ОДЗ (-∞;9) ∪ (9 ; +∞)

не відповідає умові

г)

х²-9≠0

х²≠9

х≠±3

не відповідає умові

Вірна відповідь : а

$\frac{x-2}{x^{2}+9 }$

ПОКАЗАТЬ ОТВЕТЫ

яильяатыилья 24.07.2020 13:41

а)

Пошаговое объяснение:

Перевод: Который из выражений имеет смысл при любом значении х?

Решение. Если некоторое выражение имеет смысл при любом значении х, то область допустимых выражений совпадает с осью Ох. Последнее означает, что ОДЗ равен (-∞; +∞).

Поэтому определим ОДЗ каждого выражения:

а)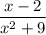 $\dfrac{x-2}{x^{2} +9}$ - знаменатель x²+9≥9>0, поэтому ОДЗ: (-∞; +∞), то есть выражение имеет смысл при любом значении х;

б)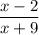 $\dfrac{x-2}{x+9}$ - при x=-9 знаменатель рана 0, поэтому ОДЗ: (-∞; -9)∪(-9; +∞), то есть выражение имеет смысл не для любого значения х;

в)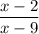 $\dfrac{x-2}{x-9}$ - при x=9 знаменатель рана 0, поэтому ОДЗ: (-∞; 9)∪(9; +∞), то есть выражение имеет смысл не для любого значения х;

г)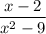 $\dfrac{x-2}{x^{2} -9}$ - при x=±3 знаменатель рана 0, поэтому ОДЗ: (-∞; -3)∪(-3; 3)∪(3; +∞), то есть выражение имеет смысл не для любого значения х.