Який периметр трикутника, якщо він обмежений осями координат та прямою y=2x+6?

Ответы

loxsanya2017 01.12.2020 22:10

$P=9+3\sqrt{5}$

Пошаговое объяснение:

Т.к. треугольник ограничен координатными осями, то это прямоугольный треугольник.

Катетами такого треугольника будут отрезки, отсекаемые графиком функции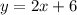 y=2x+6 . Найдем длины этих катетов

Длина катета по оси OX:

L_x = |(y-6):2| = |(0-6):2| = |-3| = 3

Длина катета по оси OY:

L_y = |2x+6| = |0+6| = 6

Длину гипотенузы найдем из теоремы Пифагора:

$L=\sqrt{L_x^2+L_y^2} =\sqrt{3^2+6^2}=\sqrt{9+36} =\sqrt{45} =3\sqrt{5}$

И тогда периметр равен:

$P=L_x+L_y+L=3+6+3\sqrt{5} =9+3\sqrt{5}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

дияр22 18.11.2020 09:47

liza1329 18.11.2020 09:47

Kurakluk 18.11.2020 09:47

кисел5467 18.11.2020 09:47

Решите уравнения 2х=0 ; -8,9 *(х-2,5)=0 ; (х+34)* (-12)-=0...

DogyStyleee 18.11.2020 09:47

dmmkuplinov 18.11.2020 09:47

393.Найдите значение суммы:...

илья1957 12.02.2020 12:24

Сколько будет(1000×190): 200+68756(985: 564) и это...

huhrova23 12.02.2020 12:25

ososkovaluba 12.02.2020 12:25

Kam09 12.02.2020 12:25

Який периметр трикутника, якщо він обмежений осями координат та прямою y=2x+6?​