Які два числа треба вставити між числами 2 і 54 щоб вони разом з диними числами утворювали геометричну прогресію

Ответы

Анастасия8383 27.08.2020 22:00

ответ: 6 и 18.

Пошаговое объяснение:

b₁=2 b₄=54 b₂=? b₃=?

b₄/b₁=b₁q³/b₁=q³=27=3³

q³=3³

q=3 ⇒

b₂=b₁q=2*3=6

b₃=b₁q²=2*3²=2*9=18.

ПОКАЗАТЬ ОТВЕТЫ

zuzin77 27.08.2020 22:00

Статус "умный, но не внимательный" ))). Я прочитал,что между 2 и 54 вставить одно число. Увы мне, увы!

Мой ответ имеет чисто "научное исследование", и не имеет отношения к данной задаче!

$3\sqrt{3}$

Пошаговое объяснение:

Обозначим второе число нашей прогрессии через х, коэффициент геометрической прогрессии обозначим через k, тогда :

первый член прогрессии: 2;

второй член прогрессии: х;

третий член прогрессии х*k=54

Но второй член прогресс можно записать и так: х = 2 * k; 2 = x/k.

Разделим третий член прогрессии на первый:

54/2=(х*k)/(x/k);

27 = k^2 (естественно, между двумя четными или двумя нечетными последовательными членами прогрессии разница в k*k=k^2 раз).

Ну а теперь решим уравнение:

k^2=27;

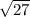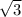k1 = $\sqrt{27}$ = 3 $\sqrt{3}$ ;

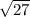k2 = - $\sqrt{27}$ = -3 $\sqrt{3}$ ;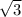

Т.к. все члены прогрессии у нас положительные, то корень k2 не подходит.

Проверяем:

n1 = 2;

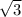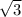n2 = 2*3* $\sqrt{3}$ = 6

n3 = 6 $\sqrt{3}$ * 3

Бинго! Получилось.

Если тебе уже известно свойство "между двумя четными или двумя нечетными последовательными членами прогрессии разница в k*k=k^2 раз" то можно обойтись и без уравнения (это уравнение есть доказательством этого свойства).

А просто выполнить действия k=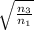 $\sqrt{\frac{n_{3} }{n_{1} } }$ ;