Y=√x(x-5)²(2-x)
найдите область определения с интервалов
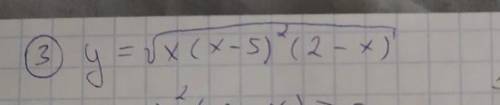
Другие вопросы по теме Математика
Популярные вопросы
- Осуществить превращение ! сн4-- с2н2-- с6н6-- со2-- со-- fе-- feсl3--...
3 - Какая масса кремния должна образоваться при востановлении магнием 30...
3 - Массовая доля углерода в алкене составляет 81,71% относительная плотность...
2 - Всем, всю сама сделала,а говорю сейчас вам просто то что вы лучшие, всем...
2 - Нужно перевести в косвенную речь) 1)james says to mary, i haven t seen...
3 - Попробуйте сочинить стихотворение с несклоняемыми существительными...
3 - Камень - разобрать на части слова (то есть корень, суффикс и т.д.)...
2 - Внимание: первый,кто решит , у того будет лучшее решение! , надо.внизу...
3 - Выберите три правельных ответа: головной мозг рыб включает отделы - 1)спинной...
1 - Make these sentences passive. 1.you make me laugh.2she never lest me...
1
Пошаговое объяснение:
область определения x(x-5)²(2-x)≥0
решаем x(x-5)²(2-x)=0 ⇒ х₁ = 0; х₂=2; х₃ = 5
получили 4 интервала. смотрим знак функции на каждом интервале
(-∞;0) y(-1)=-1*(-6)²(1+2) < 0 интервал не подходит
[0; 2] y(1) = 1(-4)²(-1+2) > 0; y(0)=0; y(2)=0 интервал подходит
(2; 5] y(3)=3(-2)²(-1) <0; y(5) =0; интервал не подходит, точка х = 5 подходит
(5; +∞) y(6) = 6*1²*(-4) < 0 интервал не подходит
ответ х ∈ [0; 2] ∪ [5]
или 0≤х≤5; х=5