Y(x)=sin(e^x^2^-tgx+log_2x)
Фото прилагается
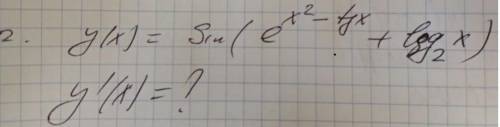
Другие вопросы по теме Математика
Популярные вопросы
- Егор потратил в интернет-магазине 2698 рублей. На покупку коврика...
1 - 1. С г. началось строительство новой засечной черты – .2. Окончание...
1 - Задача 1. Гражданину Иванову И.И. исполнилось 61 год 1 марта 2019...
3 - Можно ли по внешнему виду оленя определить условия окружающей его...
1 - Составьте краткую характеристику шведской модели социализма. 1.Период...
3 - 1. Запиши, з чим порівнює поетеса Ганна Чубач портрет бабусі у...
2 - У якому реченні вставне слово активізує увагу слухачів (тичачів)...
1 - Составьте уравнения реакция (задания на фото)...
2 - Нарисуйте схему электрической цепи, состоящей из гальванического...
3 - Як описує героїню Барбара Космовська?...
1
Пошаговое объяснение:
1). производная сложной тригонометрической функции
y'=(sin(kx+b))'=cos(kx+b)'×(kx+b)'
2). производная сложной показательной функции:
y'=(e^(kx+b))'=e^(kx+b)×(kx+b)'
3). производная тригонометрической функции:
у'=(tgx)'=1/(cos^2 x)
4). производная логарифмической функции:
у'=(log_a x)'=1/(x ×ln a)