Y=(x-1)*e^x исследовать функцию и построить её график?
Другие вопросы по теме Математика
Популярные вопросы
- (4 целых5\12-3 целых 7\18): 9,25+пять шестых (0,4+одна восьмая+0,75)...
2 - Как найти учителя по в бугульме подскажите нужно...
2 - Звуко - буквенный разбор на слову грамота...
3 - Подобные слагаемые -9x+3y+4x+y заранее...
1 - Почему умер прокурор в поэме мертвые души? и как автор относится к...
2 - Ученица за 24 минуты набирает 3 страницы.за сколько времени она наберёт...
1 - Вычислите массу гидрооксида железа (iii),который потребуется для получения...
1 - Найди лишнее слово слагаемое,уменьшаемое,вычитаемое,...
2 - Глаголы увидеть и услышать записать в формах времени единственного...
3 - Сколько корней имеет уравнение,объясните решение. x4(степени)=x+4...
3
Дана функция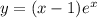
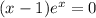 ⇔ x = 1
⇔ x = 1
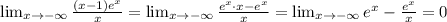 , так как e^-∞ это ноль, а также экспонента убывает(возрастает) быстрее, чем икс, значит e^x = o(x) (о-малое) значит предел равен нулю. Найдём также предел
, так как e^-∞ это ноль, а также экспонента убывает(возрастает) быстрее, чем икс, значит e^x = o(x) (о-малое) значит предел равен нулю. Найдём также предел 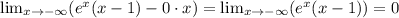 , значит есть асимптота y = 0. При х стремящимся к + бесконечности у нас пределы равны бесконечности, значит других асимптот нет. При х = 0 функция принимает значение
, значит есть асимптота y = 0. При х стремящимся к + бесконечности у нас пределы равны бесконечности, значит других асимптот нет. При х = 0 функция принимает значение 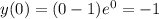 .
.
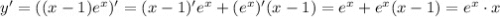
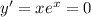 ⇔ x = 0. Так как перед старшей степенью икса стоит +, то знаки будут чередоваться справа налево начиная с плюса, выходит что точка х = 0 точка минимума, значение в ней было посчитано
⇔ x = 0. Так как перед старшей степенью икса стоит +, то знаки будут чередоваться справа налево начиная с плюса, выходит что точка х = 0 точка минимума, значение в ней было посчитано
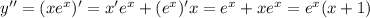
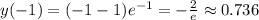 . Мы провели все рассуждения для построения графика (он на фото. Синяя прямая проведена для наглядности, чтобы показать, где конкретно точка перегиба)
. Мы провели все рассуждения для построения графика (он на фото. Синяя прямая проведена для наглядности, чтобы показать, где конкретно точка перегиба)
Нули функции
Найдём также когда y>0 и y <0. Исходя из одной точки пересечения с осью икс, y<0 при x<1, y>0 при x>0
Асимптоты:
Рассмотрим теперь производную функции:
Найдём нули производной
Найдём вторую производную:
Ноль второй производной это x = -1, аналогично Так как перед старшей степенью икса стоит +, то знаки будут чередоваться справа налево начиная с плюса, значит x = - 1 точка перегиба и при x < - 1 функция выпукла вверх, а при x > -1 функция выпукла вниз. Значение в точке х = -1 равно