Y=
знайти похідну функції
Другие вопросы по теме Математика
Популярные вопросы
- Докажи, что если два отрезка ab и cd делятся в точке их пересечения пополам, то...
3 - На тему друзья про собаку и мальчика...
2 - Напишите что то про дятла только на украинском языке....
2 - Есть ли здесь обособленные второстепенные чл. пред. ? и подчеркните грамматическую...
3 - От какого слова образовалось слово заглавие...
2 - Опишите комнату у городничего где жил хлестаков. кто по очереди и сколько дал денег...
1 - 20 ів! написати есе на тему що робить мене щасливою...
3 - Основные внешней политики 1880-1890-е годы(европа,средняя...
3 - Над болотом с шумом поднялась стая уток синтаксический разбор!...
3 - Вчём сюжет фэнтези хоббит или туда и обратно?...
2
По формуле: (f*g)'=f'*g+f*g'
Производная сложной функции (1):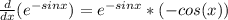
Производная от сложной функции (2):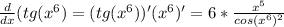
Получаем: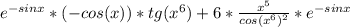
Надеюсь, что так. Удачи в учёбе, мой друг!